Contents
Gateway to MaKR library. Separated from the MaKR private (blue) area.

Favorite Books

Most favorite

  • Mathematical Elasticity by P.G.Ciarlet -- The notations on the website is based on this book.
  • Direct Methods in the Theory of Elliptic Equations, by Necas,J.--Much written about Sobolev spaces defined in Lipschitz boundary
  • Elliptic Partial Differential Equations of Second Order(1998) by Gilbarg, D. and Trudinger, N. S.-- Text book of PDEs
  • Sobolev Spaces 1st ed. by Adams, R,A.-- Sobolev spaces defined on unbounded domains and iterpolations
  • Inequalities in Mechanics and Physics, Duvaut, G. and Lions, J.L. --Book on continuum mechanics
  • Mathematical elasticity Vol.1 -- 3D Elasticity by Ciarlet, P.G. -- My foundation on Elasticity
  • Elliptic Problems in Domains with Piecewise Smooth Boundaries, by Nazarov, S.A. and Plamenevsky, B.A --Dealing with crack problems and J-integral (Cherepanov-Rice integral)
  • Non-Homogeneous Boundary Value Problems and Applications, by J.L.Lions and E.Magenes -- Interpolations of Sobolev spaces
  • Singularities in Boundary Value Problems by Grisvard, P. -- Introductory book on solutions of PDEs with singularity in domains with corner
  • Introduction fo Shape Sensitivity by Sokolowski, J.and Zolesio, J.-P,--Introduction to shape sensitivity analysis
    • }
  • Nonlinear Functional Analysis and its Applications II/A, by Zeidler. E. -- Linear Monotone Operators
    • Nonlinear Functional Analysis and its Applications II/B, by Zeidler. E. -- Noninear Monotone Operators}
  • Nonlinear Functional Analysis and its Applications III, by Zeidler. E. -- Variational Methods and Optimization
  • Nonlinear Functional Analysis and its Applications IV, , by Zeidler. E. -- Applications to Mathematical Physics

They are books that I often refer to, and many of them were read during graduate school. Most of them are purchased as electronic books or scanned and used.

Top

PDEs

  • Functional Analysis, by Yoshida K. -- Basic book of functional analysis
  • Solution of Variational Inequalities in Mechanics, by Hlavacek.I. and J. Haslinger, J., Necas, J. and Lovlsek, J.-- Unilateral Problems, One-sided contact, Plasticity

Top

Continuum Mechanics and Shape Optimization

  • Comception optimale de structures.pdf, by Allaire, G.-- Numerical examples I used
  • Perturbation+Analysis+of+Optimization+Pr.pdf, by Bonnans, J.F. and Shapiro, A.
  • Topological Derivatives in Shape Optimization, by Novotny, A.A. and Sokolowski,J.-- Textbook of topological derivatives, Eshelby's
  • Topology Optimization, by M.P. Bends$\phi $e, M.P. and Sigmund, O.-- Text about "What is topology optimization"
  • Shape sensitivity analysis via minmax differentiability, by Delfour.M.C.ssnf . Zoléio -- Important paper to refer to when dealing with the Lagrange multiplier method
  • Homogenization and Porous Media, by Allaire, G., Arbogast, T., Auriault, J.L. and Bourgeat. A.-- I want to target Porous Media in the future
  • Numerical analysis and optimization, Allaire, G.-- Textbook
  • Thermal Stresses-Advanced Theory and Applications, by Hetnarski, R.B. and Eslami, M.R.-- For the future
  • Topological Derivatives in Shape Optimization by A.A.Novotny and J. Sokolowski-- 2.5 Eshelby Energy-Momentum Tensor

Top

Geometry

  • Elementary Differential Geometry, by Pressley, A.-- In 3-d fracture, Geodesic coordinates is used.
Top

Numerical Analysis (FEM)

  • Finite element analysis using Mathematical programming language FreeFem++ in Japanese,by Ohtsuka, K. and Takaishi, T.-- Basics of FreeFEM programming and applications to continuum mechanics, shape optimization by GJ-integral, reaction-diffusion system
  • Theory and Practice of FiniteElements, Em, A. and Guermond,J.-L.-- From theory to notes on coding

Top

Fracture

  • Fracture Mechanics - Inverse Problems and Solutions, by Bui, H.D. -- Short summary of cracked materials, non-homogeneous materialss, composite materials, dissimilar interface, etc.
  • Mathematical and Computational Analyses of Cracking Formation. by Sumi, Y. -- Theoretical researches in Fracture mechanics
  • Analysis of Cracks in Solids, by Khludnev, A.M. and Kovtuenko, V.A.-- Variational methods in Crack problems
  • Multiscale modeling in continuum mechanics and structured deformations, Energy Minimization for Isotropie Nonlinear Elastic Bodies by M. Silhavy; Variational Problems of Crack Equilibrium and Crack Propagation by Le,K.G; Griffith Theory Revisited by Marigo, J.-J.; Foundations of the Theory of Structured Deformations by Piero. G.D.;　Second-Order Structured Deformations: Approximation Theorems　by Paroni，R.; Crystalline Plasticity and Structured Deformations by Deseri, L.; Elastieity with Disarrangements by Owen, D.R.

Shape optimization

  • Shape Optimization Problems by H.Azegami, H1-gradient method
  • Introduction fo Shape Sensitivity by Sokolowski, J.and Zolesio, J.-P,--Hadamard formula
  • Optimal Shape Design for Elliptic Systems by Olivier Pironneau

Top

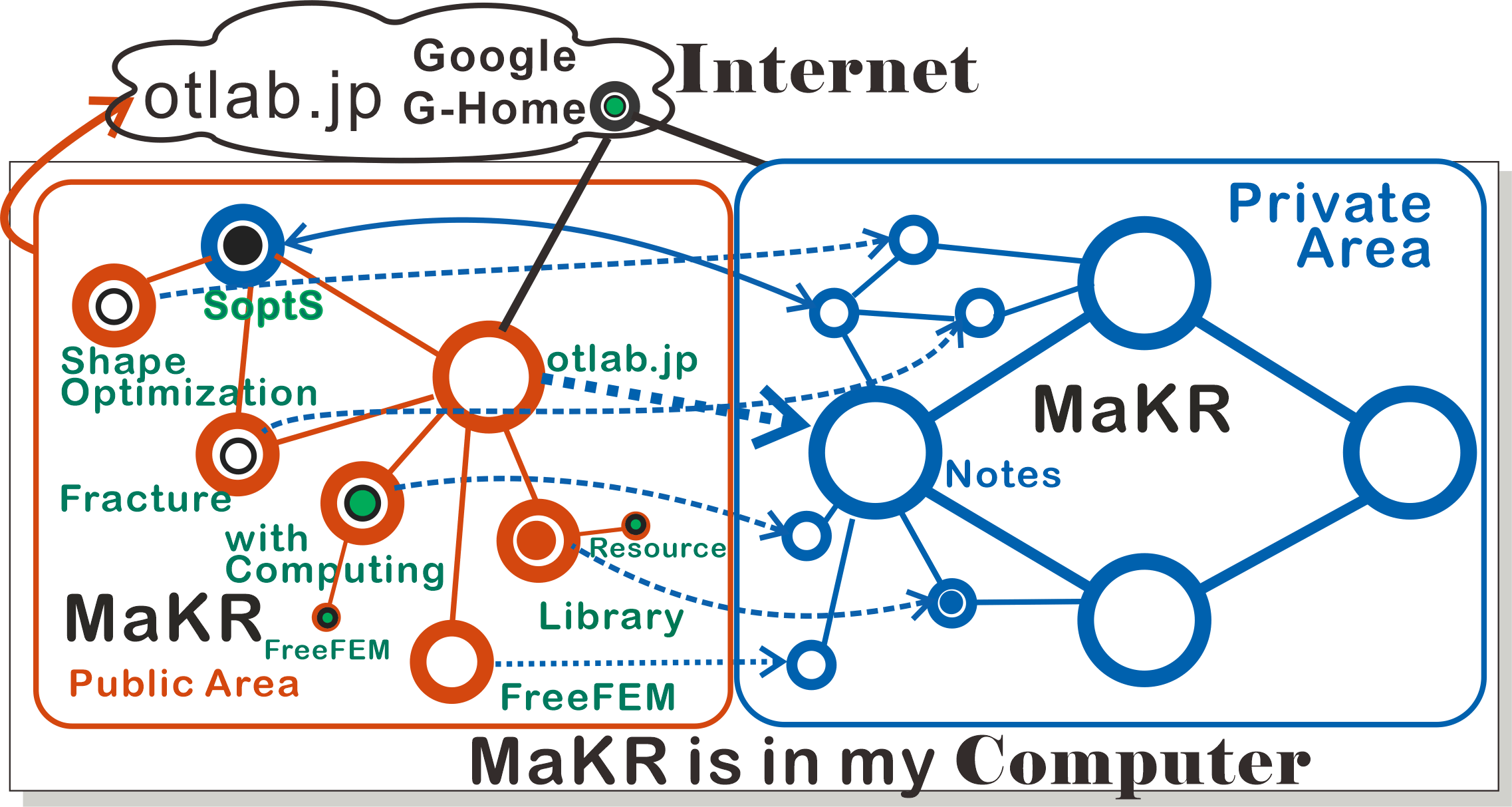
Information about the page: The current position is orange filled circle circle in the diagram below. Blue is the My favorite books in Library and orange is a duplicate for public use, where dashed line means the intrface to the Library in private.

Top

References

Literature referred to in SoptS research.

top


[Adams] R.A.Adams, Sobolev spaces, Academic Press, 1975.
[A-P06] G. Allaire and O. Pantz, Structural optimization with FreeFem++, Struct. Multidiscip. Opt, 32 (2006), 173--181.
[Al07] G. Allaire, Conception optimale de structures, Springer, 2007.
[Az94] H. Azegami, Solution to domain optimization problems, Trans. Japan Soc. Mech. Engrs. Series A, 60, No.574 (1994), 1479--1486. (in Japanese)
[A-W96] H. Azegami and Z. Wu, Domain optimization analysis in linear elastic problems: Approach using traction method, JSME Inter. J. Series A, 39 (1996), 272--278.
[Az17] H. Azegami. Solution of shape optimization problem and its application to product design, Mathematical Analysis of Continuum Mechanics and Industrial Applications, Springer, 2017, 83--98.
[B-S04] M.P. Bends{\o }e and O. Sigmund, Topology optimization: theory, methods, and applications, Springer, 2004.
[Bu04] H.D. Bui, Fracture mechanics -- Inverse problems and solutions, Springer, 2006.
[Ch67] G.P. Cherepanov, On crack propagation in continuous media, Prikl. Math. Mekh., 31 (1967), 476--493.
[Cir88] P.G. Ciarlet, Mathematical elasticity: Three-dimensional elasticity, North-Holland, 1988.
[Co85] R. Correa and A. Seeger, Directional derivative of a minimax function. Nonlinear Anal., 9(1985), 13--22.
[D-Z88] M.C. Delfour and J.-P. Zolésio, Shape sensitivity analysis via min max differentiability, SIAM J. Control and Optim., 26(1988), 834--862.
[D-D81] Ph. Destuynder and M. Djaoua, Sur une interprétation de l'intégrale de Rice en théorie de la rupture fragile. Math. Meth. in Appl. Sci., 3 (1981), 70--87.
[E-G04] A. Em and J.-L. Guermond, Theory and practice of finite elements, Springer, 2004.
[Es56] J.D. Eshelby, The Continuum theory of lattice defects, Solid State Physics, 3 (1956), 79--144.
[F-O78] D. Fujiwara and S. Ozawa, The Hadamard variational formula for the Green functions of some normal elliptic boundary value problems, Proc. Japan Acad., 54 (1978), 215--220.
[G-S52] P.R. Garabedian and M. Schiffer, Convexity of domain functionals, J.Anal.Math., 2 (1952), 281--368.
[Gr21] A.A. Griffith, The phenomena of rupture and flow in solids, Phil. Trans. Roy. Soc. London, Series A 221 (1921), 163--198.
[Gr24] A.A. Griffith, The theory of rupture, Proc. 1st.Intern. Congr. Appl. Mech., Delft (1924) 55--63.
[Gr85] P. Grisvard, Elliptic problems in nonsmooth domains, Pitman, 1985.
[Gr92] P. Grisvard, Singularities in boundary value problems, Springer, 1992.
[Had68] J. Hadamard, Mémoire sur un problème d'analyse relatif à l'équilibre des plaques élastiques encastrées, Mémoire des savants étragers, 33 (1907), 515--629.
[Hau86] E.J. Haug, K.K. Choi and V. Komkov, Design sensitivity analysis of structural systems, Academic Press, 1986.
[ffempp] F. Hecht, New development in freefem++. J. Numer. Math. 20 (2012), 251--265. 65Y15, (FreeFem++ URL:http://www.freefem.org)
[Kato] T. Kato, Perturbation theory for linear operators, Springer, 1980.
[K-W06] M. Kimura. and I. Wakano, New mathematical approach to the energy release rate in crack extension, Trans. Japan Soc. Indust. Appl. Math., 16(2006) 345--358. (in Japanese) \bibitem {K-W11} M. Kimura and I. Wakano, Shape derivative of potential energy and energy release rate in rracture mechanics, J. Math-for-industry, 3A (2011), 21--31.
[Kne05] D. Knees, Regularity results for quasilinear elliptic systems of power-law growth in nonsmooth domains: boundary, transmission and crack problems. PhD thesis, Universität Stuttgart, 2005. http://elib.uni-stuttgart.de/opus/volltexte/2005/2191/.
[Ko06] V.A. Kovtunenko, Primal-dual methods of shape sensitivity analysis for curvilinear cracks with nonpenetration, IMA Jour. Appl. Math. 71 (2006), 635--657.
[K-O18] V.A. Kovtunenko and K. Ohtsuka, Shape differentiability of Lagrangians and application to stokes problem, SIAM J. Control Optim. 56 (2018), 3668--3684.
[M-P01] B. Mohammadi and O. Pironneau, Applied shape optimization for fluids. Oxford University Press, 2001.
[Na94] S.Nazarov and B.A.Plamenevsky, Elliptic problems in domains with piecewise smooth boundaries, de Gruyter Expositions in Mathematics 13. Walter de Gruyter \& Co., 1994.
[Nec67] J. Nečas, Direct methods in the theory of elliptic equations, Springer, 2012. Translated from ``Méthodes directes en théorie des équations elliptiques, 1967, Masson''.
[Noe18] E. Noether, Invariante variationsprobleme, göttinger nachrichten, Mathematisch-Physikalische Klasse (1918), 235--257.
[N-S13] A.A. Novotny and J. Sokolowski, Topological derivatives in shape optimization, Springer, 2013.
[Oh81] K. Ohtsuka, Generalized J-integral and three dimensional fracture mechanics I, Hiroshima Math. J., 11(1981), 21--52.
[Oh85] K. Ohtsuka, Generalized J-integral and its applications. I. -- Basic theory, Japan J. Appl. Math., 2 (1985), 329--350.
[O-K00] K. Ohtsuka and A. Khludnev, Generalized J-integral method for sensitivity analysis of static shape design, Control \& Cybernetics, 29 (2000), 513--533.
[Oh02] K. Ohtsuka, Comparison of criteria on the direction of crack extension, J. Comput. Appl. Math., 149 (2002), 335--339.
[Oh02-2] K. Ohtsuka, Theoretical and numerical analysis on 3-dimensional brittle fracture, Mathematical Modeling and Numerical Simulation in Continuum Mechanics, Springer, 2002, 233--251.
[Oh09] K. Ohtsuka, Criterion for stable/unstable quasi-static crack extension by extended griffith energy balance theory, Theor. Appl. Mech. Japan, 57 (2009), 25--32.
[Oh12] K. Ohtsuka, Shape optimization for partial differential equations/system with mixed boundary conditions, RIMS K\^oky\^uroku 1791 (2012), 172--181.
[OT-K12] K. Ohtsuka and M. Kimura, Differentiability of potential energies with a parameter and shape sensitivity analysis for nonlinear case: the p-Poisson problem, Japan J. Indust. Appl. Math., 29 (2012), 23--35.
[Oh14] K. Ohtsuka and T. Takaishi, Finite element anaysis using mathematical programming language FreeFem++, Kyoritsu Shuppan, 2014. (in Japanese)
[Oh17] K. Ohtsuka, Shape optimization by GJ-integral: Localization method for composite material, Mathematical Analysis of Continuum Mechanics and Industrial Applications, Springer, 2017, 73--109.
[Oh18] K. Ohtsuka, Shape optimization by Generalized J-integral in Poisson's equation with a mixed boundary condition, Mathematical Analysis of Continuum Mechanics and Industrial Applications II, Springer, 2018, 73--83.
[Pr10] A.N. Pressley, Elementary differential geometry, Springer, 2010.
[Ri68] J.R. Rice, A path-independent integral and the approximate analysis of strain concentration by notches and cracks, J. Appl. Mech., 35(1968), 379--386.
[Ri68-2] J.R. Rice, Mathematical analysis in the mechanics of fracture, Fracture Volume II, Academic Press, 1968, 191--311.
[Pi84] O. Pironneau, Optimal shape design for elliptic systems, Springer-Verlag, 1984.
[Sa99] J.A. Samareh, A survey of shape parameterization techniques, NASA Report CP-1999-209136 (1999), 333--343.
[Sc91] B.-W. Schulze, Pseudo-differential operators on manifolds with singularities, North-Holland, 1991.
[Sok92] J. Sokolowski and J.-P. Zolesio, Introduction to shape optimization, Springer, 1992.
[St14] K. Sturm, On shape optimization with non-linear partial differential equations, Doctoral thesis, Technische Universiltät of Berlin, 2014. https://d-nb.info/106856959X/34
[Sumi] Y. Sumi, Mathematical and computational analyses of cracking formation, Springer, 2014.
[Zei/2B] E. Zeidler. Nonlinear functional analysis and its applications II/B, Springer, 1990.
[Z-S73] O.C. Zienkiewicz and J.S. Campbell, Shape optimization and sequential linear programming, Optimum Structural Design, Wiley, 1973, 109--126.

top