Shape sensitivity of energy
Crack problems, J-integral, and GJ-integral
3-d fracture problems and GJ-integral
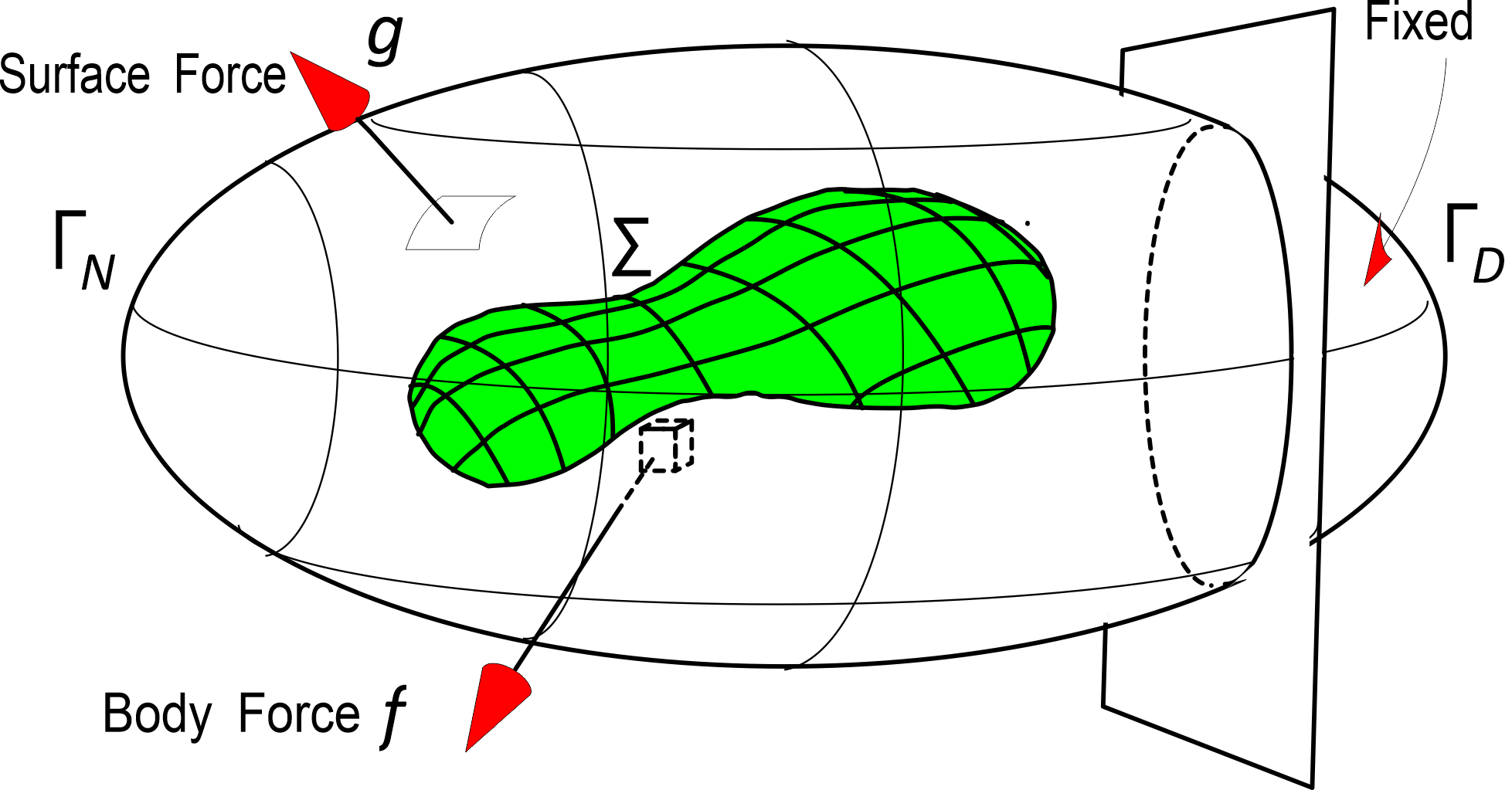
Elastic body with the crack $\Sigma $
Smooth crack extension
Here we assumed that the crack extension is smooth as follows - SC1
- There is a smooth 2-dimensional manifold $\Pi $ embedded in $\mathbb{R}^3$ such that $\Sigma (t)\subset \Pi , 0\le t\le T$.
- SC2
- $\Sigma =\Sigma (0)\subset \Sigma (t)\subset \Sigma (t')$ if $0 \lt t \lt t'$.
- SC3
- For each $t\in [0,T]$, there is a $C^{\infty }$-diffeomorphism $\phi _t:\partial \Sigma →\partial \Sigma (t)$ such that the map $[t\mapsto \phi _t]\in C^{\infty }([0,T];C^{\infty }(\partial \Sigma ;\Pi ))$.
- SC4
- The limit $\lim _{t→0}t^{-1}|\Sigma (t)-\Sigma |$ exists and nonzero.

Geodesic coordinate
We now consider the vector field $\mu _C(\gamma ), \gamma \in \partial \Sigma $ obtained from crack extension $[\gamma \mapsto \phi _t(\gamma )]$ and its extension $\mu _C(x)$ of $\mu _C(\gamma )$ defined in a neighborhood $x\in U(\partial \Sigma )$ of $\partial \Sigma $ using a geodesic coordinate perpendicular to $\partial \Sigma $ as follows. - Let $e_{\partial \Sigma ,1}(\gamma ), e_{\partial \Sigma ,2}(\gamma )$ be tangential vector fields at $\gamma \in \partial \Sigma $ on $\Pi $ such that $|e_{\partial \Sigma ,1}(\gamma )|=|e_{\partial \Sigma ,2}(\gamma )|=1$, $e_{\partial \Sigma ,2}(\gamma )$ tangent along the curve $\partial \Sigma $. Let us take $e_{\partial \Sigma ,1}(\gamma )$ in the crack extension direction and $e_{\partial \Sigma ,1}(\gamma )\perp e_{\partial \Sigma ,2}(\gamma )$.
- There is a neighborhood $\tilde{U}(\Sigma )$ of $\Sigma $ such that there is only one nearest point ${\mathcal P}(x)\in \Pi $ for all $x\in \tilde{U}(\Sigma )$. Let us denote the distance from $x$ to ${\mathcal P}(x)\in \Pi $ by $\lambda _3(x)$, that is, $$ x={\mathcal P}(x)+\lambda _3(x)e_{\Sigma ,3}({\mathcal P}(x)) e_{\Sigma ,3}(p)=-\nu (p),\, p\in \Pi $$ where $\nu (p)$ is the unit normal vector at $p\in \Pi $ in the direction from plus side to minus side of $\Pi $.
- For each $\gamma \in \partial \Sigma $, consider the geodesic curve $[\lambda \mapsto g_{\Sigma }(\gamma ,\lambda )]$ satisfying the second order differential equation (the geodesic equation) with the initial conditions $$ g_{\Sigma }(\gamma ,0)=\gamma , \frac{d g_{\Sigma }}{d\lambda }(\gamma ,0)=e_{\partial \Sigma ,1}(\gamma )$$ We can take a neighborhood $U(\partial \Sigma )$ of $\partial \Sigma , U(\partial \Sigma )\subset \tilde{U}(\Sigma )$ so that there is only one point $\gamma ({\mathcal P}(x))\in \partial \Sigma $ across $\partial \Sigma $ through ${\mathcal P}(x)$ by geodesic curve perpendicularly \cite [9.5]{Pr10};We now write the length of the geodesic curve from $\gamma ({\mathcal P(x)})$ to ${\mathcal P}(x)\in \Pi $ by $\lambda _1(x)$. \li There is a number $\epsilon \gt 0$ so that the mapping \begin{equation} F_{\partial \Sigma }:(\gamma ,\lambda _1,\lambda _3)\mapsto g_{\Sigma }(\gamma ,\lambda _1)+\lambda _3e_{\Sigma ,3}(g_{\Sigma }(\gamma ,\lambda _1)) \tag{2.21} \end{equation} become 1-1 mapping from $\partial \Sigma \times (-\epsilon ,\epsilon )^2$ into $\mathbb{R}^3$. Now we replace $U(\partial \Sigma )$ with $F_{\partial \Sigma }(\partial \Sigma \times (-\epsilon ,\epsilon )^2)$. Then $F_{\partial \Sigma }$ become the diffeomorphism from $\partial \Sigma \times (-\epsilon ,\epsilon )^2$ onto $U(\partial \Sigma )$.
- Take $\omega $ so that $\overline{\omega }\subset U(\partial \Sigma )$.
- We define the velocity of crack extension at the edge of crack by \begin{equation} v_{C}(\gamma ):=\left \langle \left .\frac{d}{dt}\phi _t(\gamma )\right |_{t=0},e_{\partial \Sigma ,1}(\gamma )\right \rangle ~~ \gamma \in \partial \Sigma \tag{2.22} \end{equation} where $\langle ,\rangle $ stands for the inner product in $\mathbb{R}^3$.
- We now extend $v_C(\gamma )$ to the vector defined in $U(\partial \Sigma )$ by $$ \mu _C(x):=v_{C}(\gamma ({\mathcal P}(x)))e_{\partial \Sigma ,1}(\gamma ({\mathcal P}(x))) x\in U(\partial \Sigma )$$ .
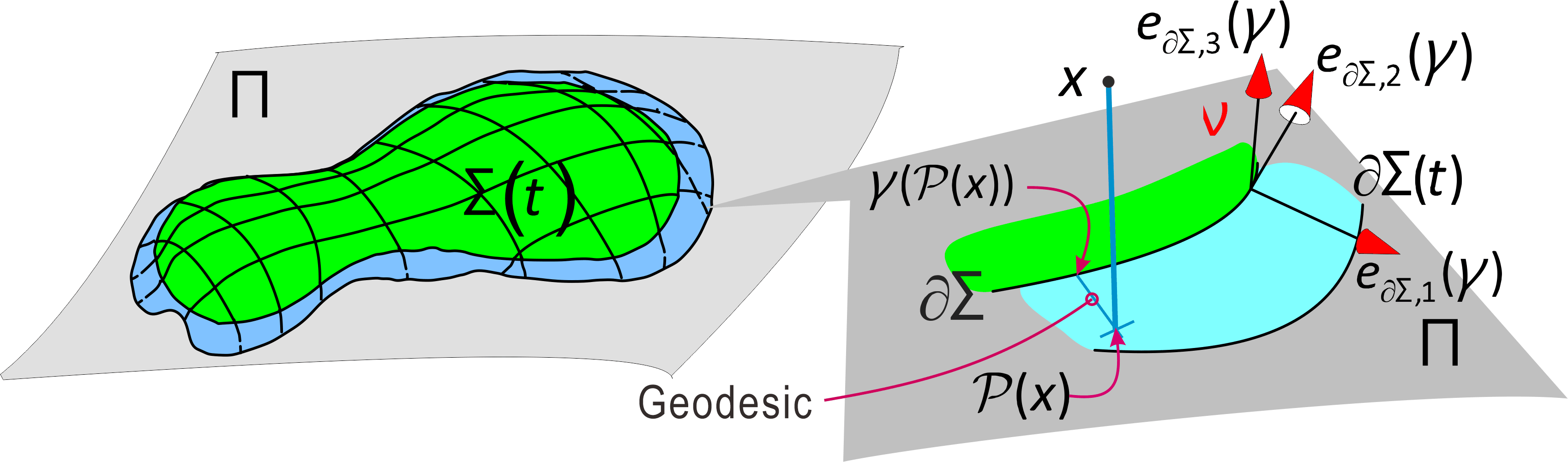
Geodesic coordinate system near the crack front $\partial \Sigma $
Theorem 2.7
For a smooth crack extension $\{\Sigma (t)\}$,
\begin{eqnarray} \mathcal{G}(f,g,\Sigma (\cdot )) &=&J_{\omega }(u,\mu _C |\partial \omega )\left (\int _{\partial \Sigma }v_{C}(\gamma )d\gamma \right )^{-1} \tag{2.23}
\end{eqnarray}
\begin{eqnarray} \mathcal{G}(f,g,\Sigma (\cdot ))&:=& \lim _{t→+0}\frac{\mathcal{E}(u;f,g,\Omega )-\mathcal{E}(u(t);f,g,\Omega (t))}{|\Sigma (t)\setminus \Sigma |_{\Pi }}\notag \tag{2.24}
\end{eqnarray} where $|\cdot |_{\Pi }$ is the surface measure on $\Pi $ and $d\gamma $ the line element of $\partial \Sigma $. 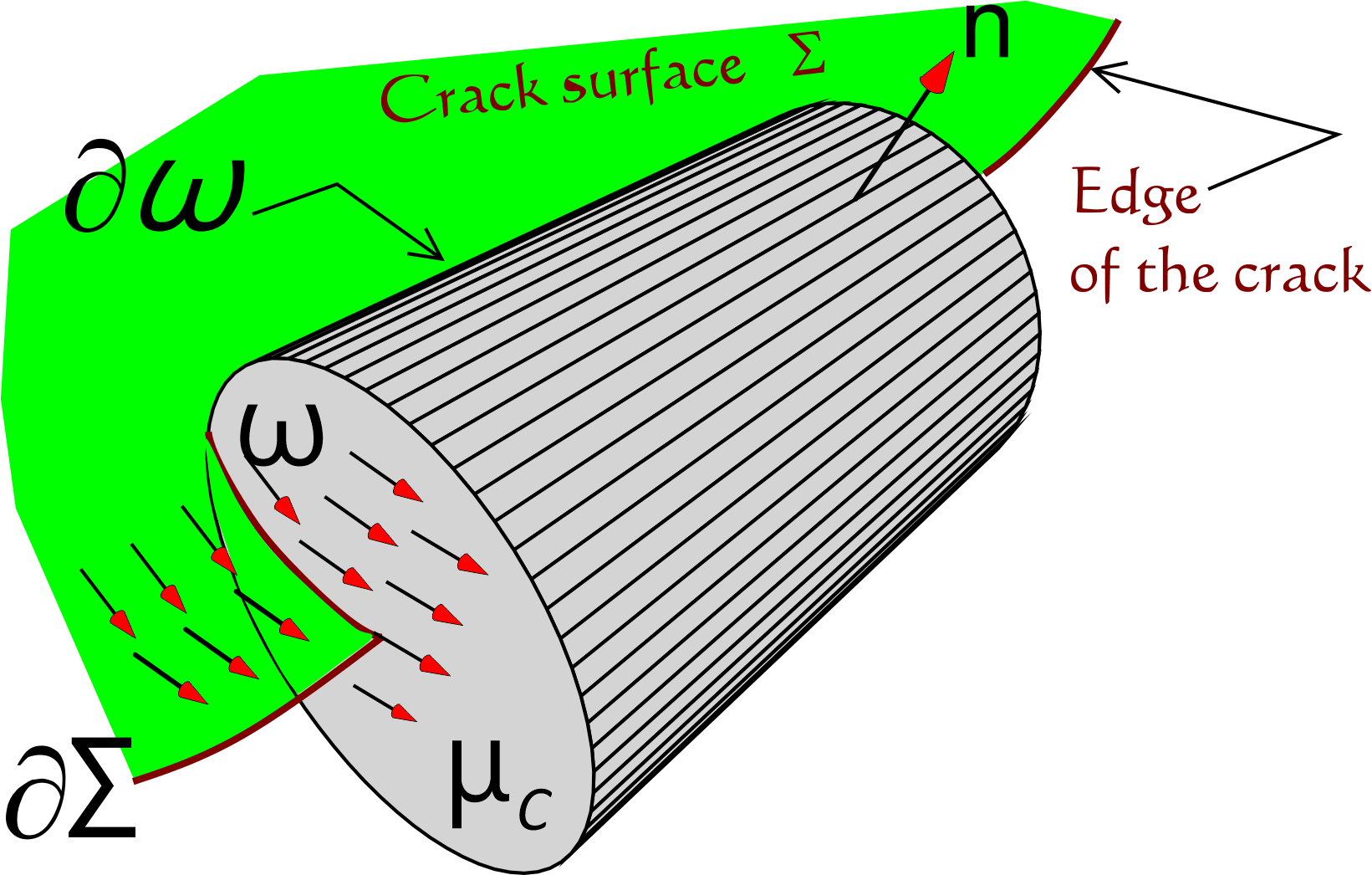
A part of a tubular neighborhood $\omega $ of the crack front $\partial \Sigma $ and the vector field $\mu _C$ obtained from the crack extension
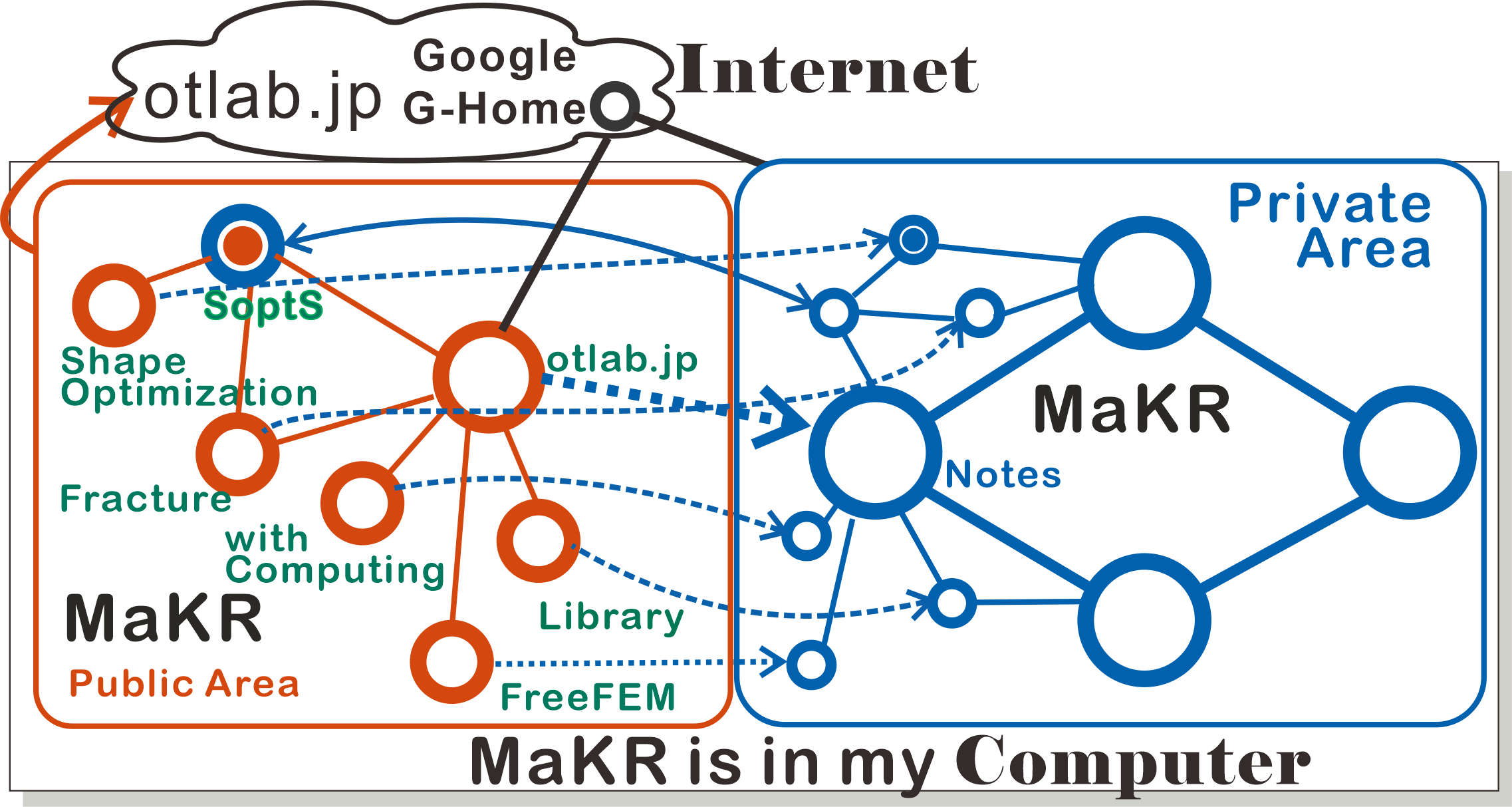
Information about the page: The current position is painted circle in the diagram below. Blue is the main MaKR and orange is a duplicate for MaKR's public use, where dashed line means the connection to the private area The dashed lines are only connections to main MaKR.