Shape optimization
Finite element analysis by the GJ-integral
In this subsection, to simplify the explanation, $\Omega $ is a polygon whose finite elements are triangles in 2-dimensional domain. Essentially the same results hold in the 3-dimensional case. In our problem, we cannot expect the smoothness of the solution $u$, but it will be able to assume the existance of a number $s, 1 \lt s \lt 2$ such that $u\in H^s(\Omega ;\mathbb{R}^m)$ (see e.g., [Gr85, Gr92, Kne05]).Triangulation
Let $\mathcal{T}_h(\Omega )=\{T_k,\, k=1,…,n_t\}$ be a triangulation of $\overline{\Omega }=\cup _{k=1}^{n_t}T_k$ with the maximum diameter $h=\max \{\textrm{diam}(T_k):\, T_k\in \mathcal{T}_h(\Omega )\}$. Let us denote by $n_v$ the number of vertices $q^l, l=1,…,n_v$ of the triangles in $\mathcal{T}_h(\Omega )$
FE-spaces
We now introduce the basis function $\phi _l,l=1,…,n_v$ such that $\phi _k(q^l)=\delta ^l_k$, that is, linear polynomial ($P_1$) on each triangle, and the P1-finite element space
\begin{eqnarray*} V_h(\mathcal{T}_h(\Omega ),P_1)&=&\{c_1\phi _1+…+c_{n_v}\phi _{n_v}\\ &&~~:\, c_i\in \mathbb{R},\, \phi _i |_K\in P_1,\, ∀K\in \mathcal{T}_h(\Omega ),\, 1\le i\le n_v\}
\end{eqnarray*} For a continuous function $v(x),x\in \overline{\Omega }$, the $P_1$-approximation $v_h\in V_h(\mathcal{T}_h(\Omega ),P_1)$ is given by $c_i=v(q^i),\, i=1,…,n_v$. Let $\Pi _hv$ be the projection of $v$ into $\Pi _hv\in V_h(\mathcal{T}_h(\Omega ),P_1)$ defined by $c_i=v(q^i),\, i=1,…,n_v$.Error estimation
Then by Taylor expansion, we can get the estimation for a smooth function $v$ (see e.g., [Coro.1.128, E-G04])
\begin{equation} \|\Pi _hv-v\|_{1,\Omega }\le Ch\|v\|_{2,\Omega } \tag{3.25}
\end{equation} The operator $v\mapsto \Pi _hv\in H^1(\Omega ;\mathbb{R}^m)$ is orthogonal projection, so the Pythagoras identity yields (see e,g,, [Lemma 1.131, E-G04]
\begin{equation} \|(I-\Pi _h)v\|_{1,\Omega }\le \|v\|_{1,\Omega } \tag{3.26}
\end{equation} Using the interpolation theory of operators [7.17,7.43, Adams], we derive from (3.25)
and (3.26)
$$ \|(I-\Pi _h)u\|_{1,\Omega }\le C^{s-1}h^{s-1}\|u\|_{s,\Omega },$$ The error between $u$ and $u_h$ is estimated by Céa's Lemma(see e.g., [Lemma 2.28, E-G04]), that is, $\|u-u_h\|_{1,\Omega }\le Ch^{s-1}$ with a constant $C \gt 0$ independent of $h$. If the problem (2.1)
is linear, then by $\widehat{W}(x,u,\nabla u)=\delta \widehat{W}(x,u,\nabla u)[u]/2$, we can prove $$ |R_{\Omega }(u,\mu )-R_{\Omega }(u_h,\mu )|\le C\left (\|f\|_{L^2(\Omega )}+\|u\|_{1,\Omega }+\|u_h\|_{1,\Omega }\right )\|u-u_h\|_{1,\Omega }\|\mu \|_{1,\infty ,\Omega }$$ with a constant $C \gt 0$ independent of $h$.\c
Error estimation of GJ-integral
So that
\begin{equation} |R_{\Omega }(u,\mu )-R_{\Omega }(u_h,\mu )|\le Ch^{s-1} \tag{3.27}
\end{equation} for $u\in H^s(\Omega ;\mathbb{R}^m), 1 \lt s \lt 2$. If $u\in H^s(\Omega ;\mathbb{R}^d), s \gt 3/2$, we can use the Hadamard formula (2.37)
, but the FE analysis in (2.37)
require an estimation of the FE-approximation like that $\|u-u_h\|_{s,\Omega }, s \gt 3/2$ by the Trace theorem (see e.g., [Theorem 5.5, Nec67]). However, even with the higher order FEM utilizing Lagrangian interpolation polynomials, we only evaluate the approximation in $H^1(\Omega ;\mathbb{R}^m)$, i.e., $\|u-u_h\|_{1,\Omega }$ (see e.g., [Coro.3.29, E-G04]). So, even if $u$ is smooth, it is difficult to improve the calculation accuracy of $P_{\Omega }(u_h,\mu )$ because $\nabla u_h$ is discontinuous on the interface $\overline{T_k}\cap \overline{T_l}$ of different meshs. For the reason just above, if we try to calculate J-integral (2.16a)
with high accuracy we encounter same problem.Crack problem and Mixed boundary condition
In crack problems (see FEM of J-integral
, Section 2.2
) and mixed boundary conditions (Section 2.5.2
), the integral $J_{\omega }(u,\mu |\partial \omega )$ appear with $\omega $ containing the edge of crack or bound parts of different boundary conditions. From Corollary 2.4
, it is possible to change $J_{\omega }(u,\mu |\partial \omega )$ to $R_{\omega _0}(u,\beta _{\omega }\mu )$ only using a cut-off function $\beta _{\omega }$ of $\omega $ such as $\beta _{\omega }=1$ on $\omega $ and $\textrm{supp}\beta _{\omega }\subset \omega _0$. Here, we notice that $J_{\omega _0}(u,\mu |\partial \omega _0)-J_{\omega }(u,\mu |\partial \omega ) ≈P_{\omega _0\setminus \overline{\omega }}(u,\mu |(\partial \Omega \cap (\omega _0\setminus \overline{\omega }))$. In a crack problem, $P_{\omega _0\setminus \overline{\omega }}(u,\mu |(\partial \Omega \cap (\omega _0\setminus \overline{\omega }))$, $\partial \Omega =\partial D\cup \Sigma $, is a integral over a crack surface $\Sigma $ except the edge and $\mu \perp n$ for the normal vector $n$ of a crack surface, then $P_{\omega _0\setminus \overline{\omega }}(u,\mu |(\partial \Omega \cap (\omega _0\setminus \overline{\omega }))=0$. However $P_{\omega _0\setminus \overline{\omega }}(u,\mu |(\partial \Omega \cap (\omega _0\setminus \overline{\omega }))$ remains in mixed boundary condition. Since the constant $C$ in (3.27)
is affected by $\nabla \beta _{\omega }$, it is difficult to bring $\omega $ closer to singular points
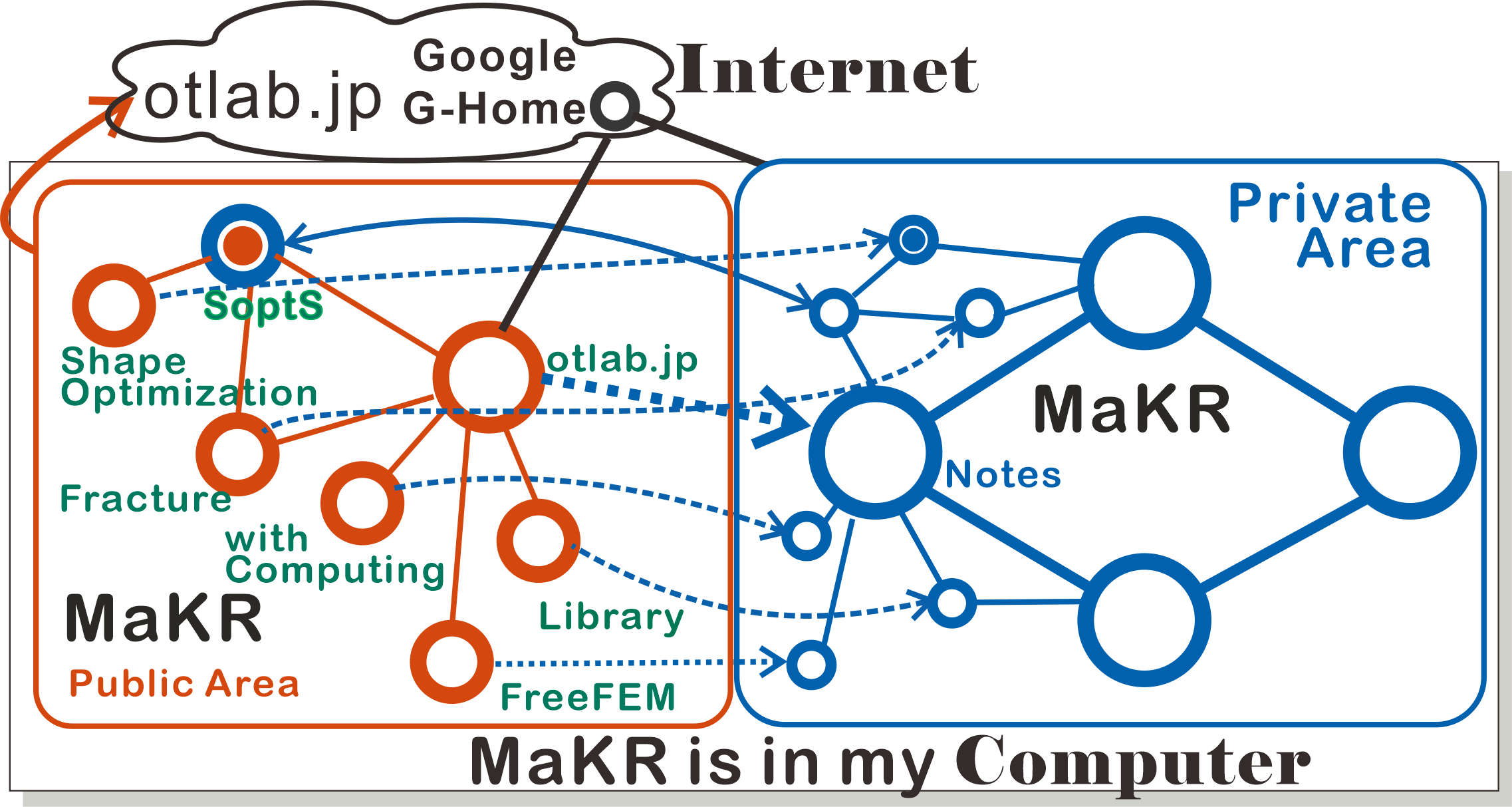
. Information about the page: The current position is painted circle in the diagram below. Blue is the main MaKR and orange is a duplicate for MaKR's public use, where dashed line means the connection to the private area The dashed lines are only connections to main MaKR.