For a given function $f\in L^2(\mathbb{R}^2)$, consider the Poisson equation $-\Delta u=f$ defined on a polygonal domain $\Omega $ with the boundary $\partial \Omega =\cup _{j=1}^{j_M}\overline{\Gamma }_j$ such that $\overline{\Gamma }_j$ is a segment and $\Gamma _j$ is open for each $j$, $\Gamma _i\cap \Gamma _j=\emptyset $ if $i\neq j$, and the segments are numbered in such way that $\Gamma _{j+1}$ follows $\Gamma _j$ according to the positive orientation except $\Gamma _{j_M+1}:=\Gamma _1$.We denote by $\gamma _j$ the endpoint of $\Gamma _j$ and by $\Theta _j$ the measure of the interior angle at $\gamma _j$. We now put $\Gamma _D=\cup _{j=1}^{j_D}\overline{\Gamma }_j\setminus \{\gamma _{j_D},\gamma _{j_M}\}$, $\Gamma _N=\cup _{j=j_D+1}^{j_M}\overline{\Gamma }_j\setminus \{\gamma _{j_D},\gamma _{j_M}\}$ and assume that $\Theta _{j_D}=\Theta _{j_M}=\pi $.

Domain removed from the neighbourhood of singular points $\Gamma _{DN}:=\{\gamma _{j_D},\gamma _{j_M}\}$

The minimizer $u\in V(\Omega )$ of (2.1) over $V(\Omega )=\{v\in H^1(\Omega ):\, v=0\textrm{ on }\Gamma _D\}$ belong to $u\in H^s(\Omega _{\epsilon })\, s \gt 3/2, \Omega _{\epsilon }=\Omega \setminus \overline{B_{\epsilon }(\Gamma _{DN})}, B_{\epsilon }(\Gamma _{DN}):=B_{\epsilon }(\gamma _{j_D}) \cup B_{\epsilon }(\gamma _{j_M})$ where $B_{\epsilon }(\gamma )=\{x:\, |x-\gamma | \lt \epsilon \}$. By a perturbation $\{\varphi _t\} _{t\in [0,T_0]}$, we have \begin{eqnarray} &&\frac{d}{dt}\mathcal{E}(u^{\varphi _t};f,0,\Omega (t))|_{t=0} =-R_{\Omega }(u;\mu _{\varphi })-\int _{\Gamma _N}fu(\mu _{\varphi }\cdot n)ds\tag{2.45}\\ && =P_{\Omega _{\epsilon }}(u,\mu _{\varphi }|\Gamma _D) +P_{\Omega _{\epsilon }}(u,\mu _{\varphi }|\Gamma _N)\notag \\ && -\sum _{\gamma \in \{\gamma _{j_D},\gamma _{j_M}\} }J_{B_{\epsilon }(\gamma )}(u,\mu _{\varphi }|\partial B_{\epsilon }(\gamma )) -\int _{\Gamma _N}fu(\mu _{\varphi }\cdot n)ds\notag \end{eqnarray} \begin{eqnarray} &&P_{\Omega _{\epsilon }}(u,\mu _{\varphi }|\Gamma _D) =-\frac{1}{2}\int _{\Gamma _D\setminus B_{\epsilon }(\Gamma _{DN})}\left (\frac{\partial u}{\partial n}\right )^2ds \tag{2.46} \end{eqnarray} \begin{eqnarray} &&P_{\Omega _{\epsilon }}(u,\mu _{\varphi }|\Gamma _N) =\frac{1}{2}\int _{\Gamma _N\setminus B_{\epsilon }(\Gamma _{DN})}|\nabla u |^2ds \tag{2.47} \end{eqnarray} Here we used that $J_{\Omega _{\epsilon }}(u;\mu _{\varphi })=0$ and $u=0$ on $\Gamma _j, 1\le j\le j_D$ and $\partial u/\partial n=0$ on $\Gamma _j, j_D \lt j\le j_M$. The solution $u$ has the structure $u |_{B_{\epsilon }(\gamma _{j_M})\cap \Omega }=K(\gamma _{j_M})S+u_R, u_R\in H^2(B_{\epsilon }(j_M)\cap \Omega )$ with a constant $K(\gamma _{j_M})$ and $S=\sqrt{r_{j_M}}\sin (\theta _{j_M}/2)$, where $(r_{j_M},\theta _{j_M})$ is the local polar coordinate with origin at $\gamma _{j_M}$; $r_{j_M}=|x-\gamma _{j_M}|$ (see e.g.[Gr92]), $\Gamma _1$ is on the half-axis $\theta _{j_M}=0$ and $\Gamma _{j_M}$ is on the half-axis $\theta _{j_M}=\pi $.

Local polar coordinate system $(r_{j_M},\theta _{j_M})$ with origin at $\gamma _{j_M}$

So then we have \begin{equation} \lim _{\epsilon →0}J_{B_{\epsilon }(\gamma _{j_M})}(u,\mu _{\varphi }| \partial B_{\epsilon }(\gamma _{j_M}))=\frac{\pi }{8} K(\gamma _{j_M})^2 (\mu _{\varphi }\cdot \tau )(\gamma _{j_M}), \tag{2.48} \end{equation} where $\tau (x)$ is the tangential vector at $x\in \partial \Omega $ with positive direction.

Theorem Poisson with mixed boundary

The shape sensitivity of energy $\frac{d}{dt}\mathcal{E}(u^{\varphi _t};f,0,\Omega (t))|_{t=0}$ with the mixed boundary condition stated just above is \begin{eqnarray} &&\lim _{\epsilon →0}\left \{P_{\Omega _{\epsilon }}(u,\mu _{\varphi }|\Gamma _D) +P_{\Omega _{\epsilon }}(u,\mu _{\varphi }|\Gamma _N)\right \} \tag{2.49} \\ &&-\frac{\pi }{8} \left \{K(\gamma _{j_M})^2 (\mu _{\varphi }\cdot \tau )(\gamma _{j_M}) -K(\gamma _{j_D})^2 (\mu _{\varphi }\cdot \tau )(\gamma _{j_D}) \right \} \notag \\ &&-\int _{\Gamma _N}fu(\mu _{\varphi }\cdot n)ds\notag \end{eqnarray} In particular in the case of $\varphi _t(\Omega )=\Omega $, the energy decreases as $\Gamma _D(t)\subset \Gamma _D$.

If $\Theta _{j_M},\Theta _{j_D} \lt \pi $, then the second term in (2.49) disappear. If $\Theta _{j_M} \gt \pi $, (2.45) is true but the existence of the limit as in (2.49) is not clear. The method used here is applicable to various boundary value problems with mixed boundary conditions.

Information about the page: The current position is painted circle in the diagram below. Blue is the main MaKR and orange is a duplicate for MaKR's public use, where dashed line means the connection to the private area The dashed lines are only connections to main MaKR.

Top

top

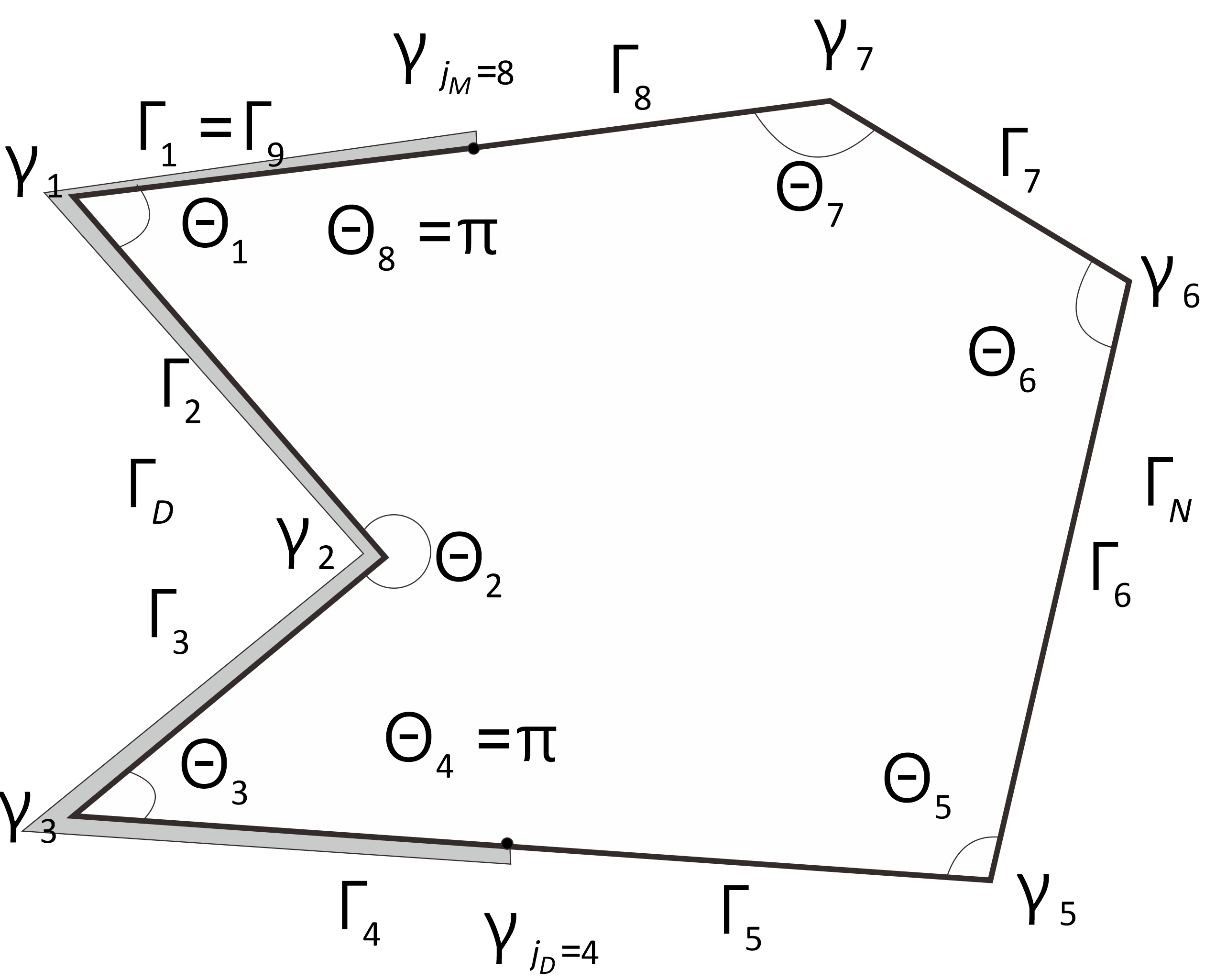
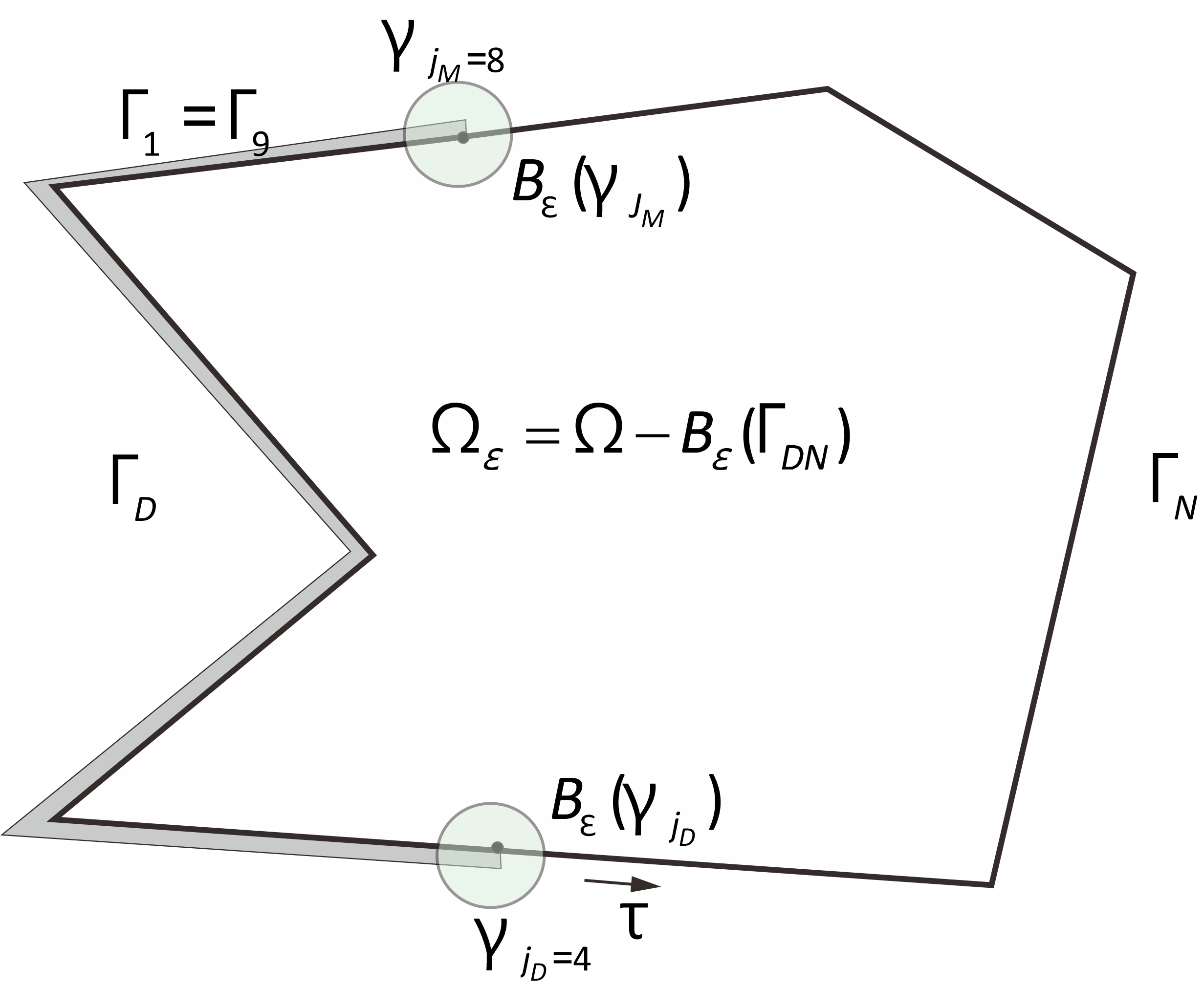
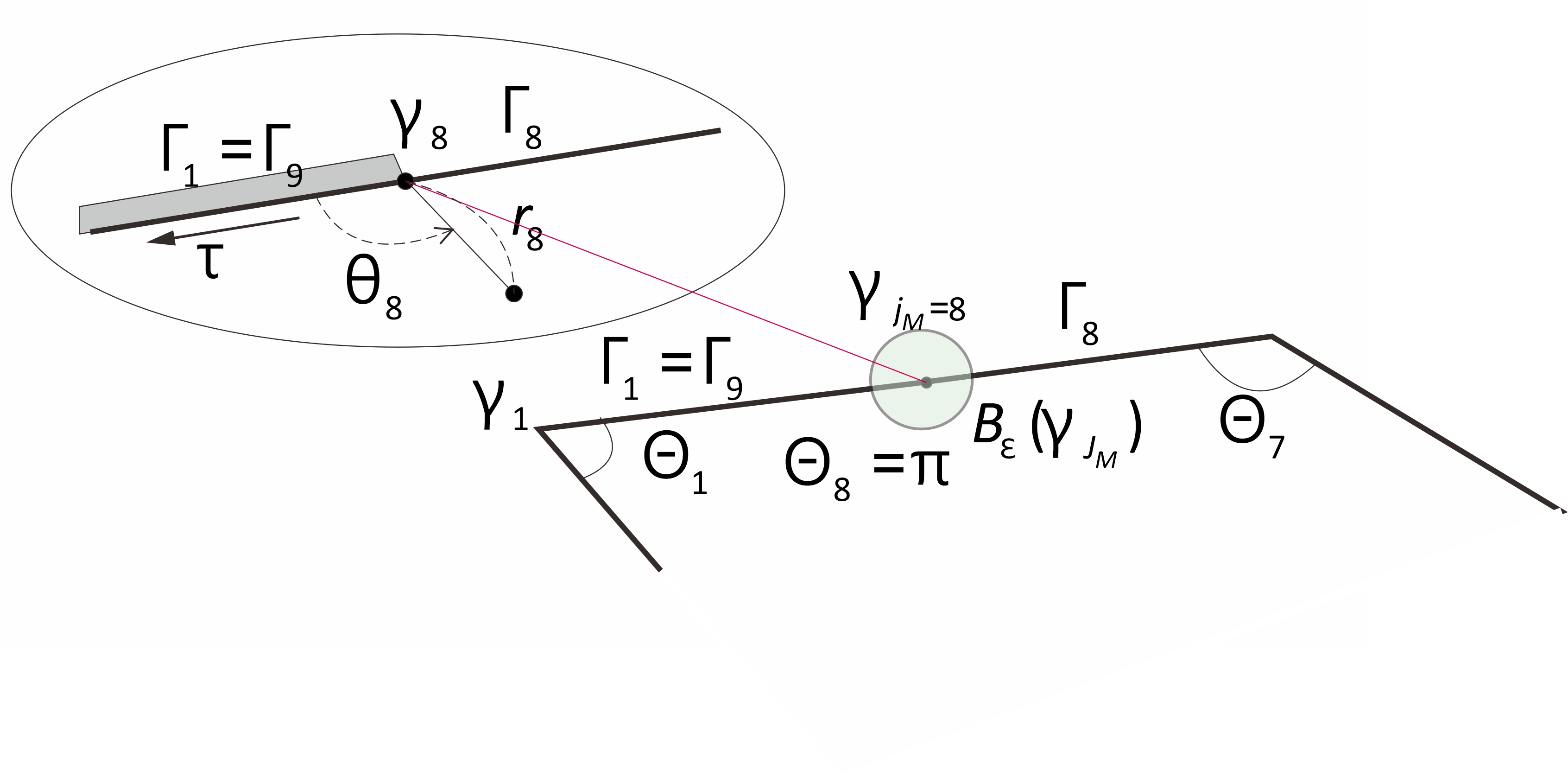
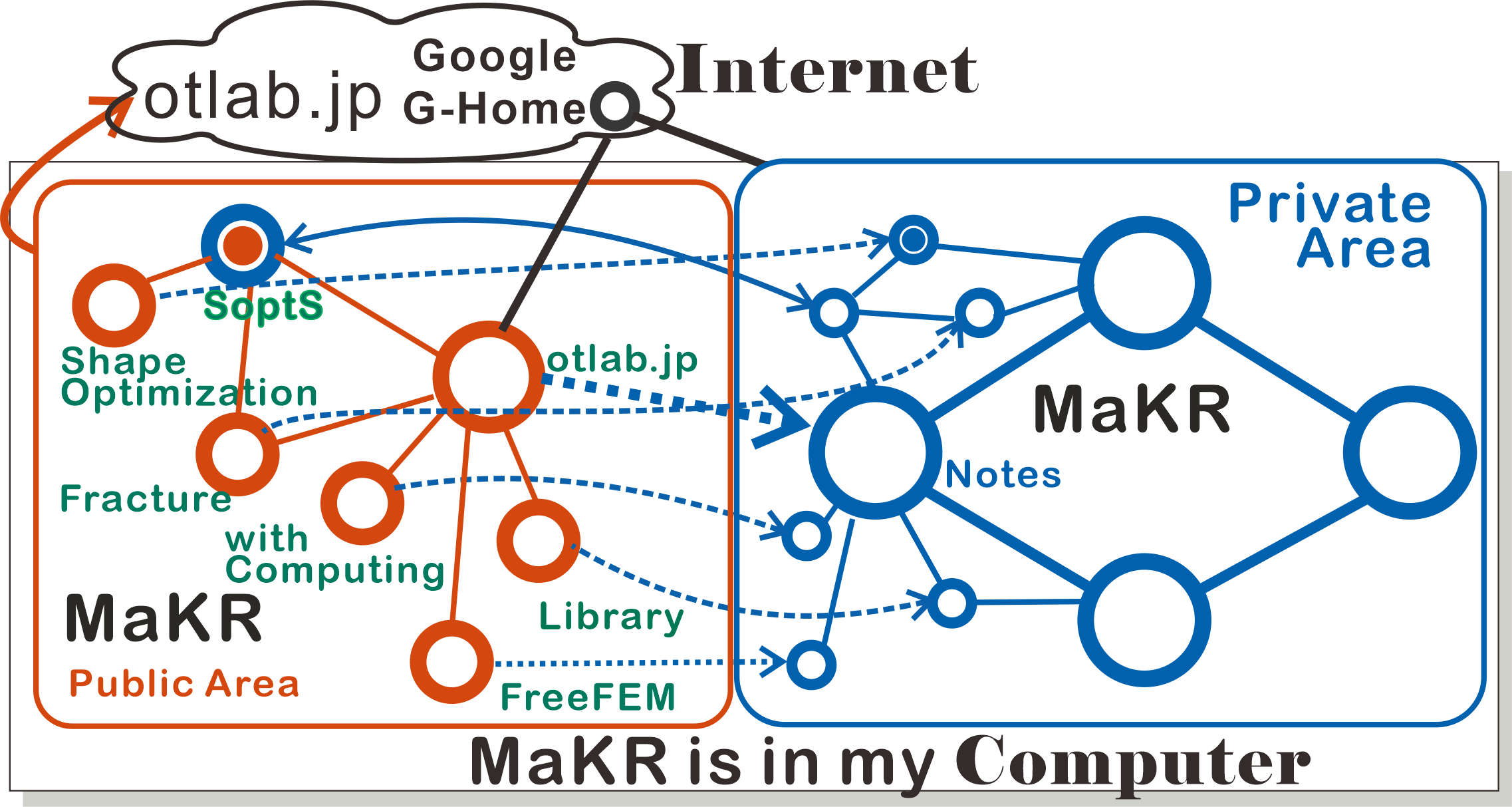
[Adams] R.A.Adams, Sobolev spaces, Academic Press, 1975.
[A-P06] G. Allaire and O. Pantz, Structural optimization with FreeFem++, Struct. Multidiscip. Opt, 32 (2006), 173--181.
[Al07] G. Allaire, Conception optimale de structures, Springer, 2007.
[Az94] H. Azegami, Solution to domain optimization problems, Trans. Japan Soc. Mech. Engrs. Series A, 60, No.574 (1994), 1479--1486. (in Japanese)
[A-W96] H. Azegami and Z. Wu, Domain optimization analysis in linear elastic problems: Approach using traction method, JSME Inter. J. Series A, 39 (1996), 272--278.
[Az17] H. Azegami. Solution of shape optimization problem and its application to product design, Mathematical Analysis of Continuum Mechanics and Industrial Applications, Springer, 2017, 83--98.
[B-S04] M.P. Bends{\o }e and O. Sigmund, Topology optimization: theory, methods, and applications, Springer, 2004.
[Bu04] H.D. Bui, Fracture mechanics -- Inverse problems and solutions, Springer, 2006.
[Ch67] G.P. Cherepanov, On crack propagation in continuous media, Prikl. Math. Mekh., 31 (1967), 476--493.
[Cir88] P.G. Ciarlet, Mathematical elasticity: Three-dimensional elasticity, North-Holland, 1988.
[Co85] R. Correa and A. Seeger, Directional derivative of a minimax function. Nonlinear Anal., 9(1985), 13--22.
[D-Z88] M.C. Delfour and J.-P. Zolésio, Shape sensitivity analysis via min max differentiability, SIAM J. Control and Optim., 26(1988), 834--862.
[D-D81] Ph. Destuynder and M. Djaoua, Sur une interprétation de l'intégrale de Rice en théorie de la rupture fragile. Math. Meth. in Appl. Sci., 3 (1981), 70--87.
[E-G04] A. Em and J.-L. Guermond, Theory and practice of finite elements, Springer, 2004.
[Es56] J.D. Eshelby, The Continuum theory of lattice defects, Solid State Physics, 3 (1956), 79--144.
[F-O78] D. Fujiwara and S. Ozawa, The Hadamard variational formula for the Green functions of some normal elliptic boundary value problems, Proc. Japan Acad., 54 (1978), 215--220.
[G-S52] P.R. Garabedian and M. Schiffer, Convexity of domain functionals, J.Anal.Math., 2 (1952), 281--368.
[Gr21] A.A. Griffith, The phenomena of rupture and flow in solids, Phil. Trans. Roy. Soc. London, Series A 221 (1921), 163--198.
[Gr24] A.A. Griffith, The theory of rupture, Proc. 1st.Intern. Congr. Appl. Mech., Delft (1924) 55--63.
[Gr85] P. Grisvard, Elliptic problems in nonsmooth domains, Pitman, 1985.
[Gr92] P. Grisvard, Singularities in boundary value problems, Springer, 1992.
[Had68] J. Hadamard, Mémoire sur un problème d'analyse relatif à l'équilibre des plaques élastiques encastrées, Mémoire des savants étragers, 33 (1907), 515--629.
[Hau86] E.J. Haug, K.K. Choi and V. Komkov, Design sensitivity analysis of structural systems, Academic Press, 1986.
[ffempp] F. Hecht, New development in freefem++. J. Numer. Math. 20 (2012), 251--265. 65Y15, (FreeFem++ URL:http://www.freefem.org)
[Kato] T. Kato, Perturbation theory for linear operators, Springer, 1980.
[K-W06] M. Kimura. and I. Wakano, New mathematical approach to the energy release rate in crack extension, Trans. Japan Soc. Indust. Appl. Math., 16(2006) 345--358. (in Japanese) \bibitem {K-W11} M. Kimura and I. Wakano, Shape derivative of potential energy and energy release rate in rracture mechanics, J. Math-for-industry, 3A (2011), 21--31.
[Kne05] D. Knees, Regularity results for quasilinear elliptic systems of power-law growth in nonsmooth domains: boundary, transmission and crack problems. PhD thesis, Universität Stuttgart, 2005. http://elib.uni-stuttgart.de/opus/volltexte/2005/2191/.
[Ko06] V.A. Kovtunenko, Primal-dual methods of shape sensitivity analysis for curvilinear cracks with nonpenetration, IMA Jour. Appl. Math. 71 (2006), 635--657.
[K-O18] V.A. Kovtunenko and K. Ohtsuka, Shape differentiability of Lagrangians and application to stokes problem, SIAM J. Control Optim. 56 (2018), 3668--3684.
[M-P01] B. Mohammadi and O. Pironneau, Applied shape optimization for fluids. Oxford University Press, 2001.
[Na94] S.Nazarov and B.A.Plamenevsky, Elliptic problems in domains with piecewise smooth boundaries, de Gruyter Expositions in Mathematics 13. Walter de Gruyter \& Co., 1994.
[Nec67] J. Nečas, Direct methods in the theory of elliptic equations, Springer, 2012. Translated from ``Méthodes directes en théorie des équations elliptiques, 1967, Masson''.
[Noe18] E. Noether, Invariante variationsprobleme, göttinger nachrichten, Mathematisch-Physikalische Klasse (1918), 235--257.
[N-S13] A.A. Novotny and J. Sokolowski, Topological derivatives in shape optimization, Springer, 2013.
[Oh81] K. Ohtsuka, Generalized J-integral and three dimensional fracture mechanics I, Hiroshima Math. J., 11(1981), 21--52.
[Oh85] K. Ohtsuka, Generalized J-integral and its applications. I. -- Basic theory, Japan J. Appl. Math., 2 (1985), 329--350.
[O-K00] K. Ohtsuka and A. Khludnev, Generalized J-integral method for sensitivity analysis of static shape design, Control \& Cybernetics, 29 (2000), 513--533.
[Oh02] K. Ohtsuka, Comparison of criteria on the direction of crack extension, J. Comput. Appl. Math., 149 (2002), 335--339.
[Oh02-2] K. Ohtsuka, Theoretical and numerical analysis on 3-dimensional brittle fracture, Mathematical Modeling and Numerical Simulation in Continuum Mechanics, Springer, 2002, 233--251.
[Oh09] K. Ohtsuka, Criterion for stable/unstable quasi-static crack extension by extended griffith energy balance theory, Theor. Appl. Mech. Japan, 57 (2009), 25--32.
[Oh12] K. Ohtsuka, Shape optimization for partial differential equations/system with mixed boundary conditions, RIMS K\^oky\^uroku 1791 (2012), 172--181.
[OT-K12] K. Ohtsuka and M. Kimura, Differentiability of potential energies with a parameter and shape sensitivity analysis for nonlinear case: the p-Poisson problem, Japan J. Indust. Appl. Math., 29 (2012), 23--35.
[Oh14] K. Ohtsuka and T. Takaishi, Finite element anaysis using mathematical programming language FreeFem++, Kyoritsu Shuppan, 2014. (in Japanese)
[Oh17] K. Ohtsuka, Shape optimization by GJ-integral: Localization method for composite material, Mathematical Analysis of Continuum Mechanics and Industrial Applications, Springer, 2017, 73--109.
[Oh18] K. Ohtsuka, Shape optimization by Generalized J-integral in Poisson's equation with a mixed boundary condition, Mathematical Analysis of Continuum Mechanics and Industrial Applications II, Springer, 2018, 73--83.
[Pr10] A.N. Pressley, Elementary differential geometry, Springer, 2010.
[Ri68] J.R. Rice, A path-independent integral and the approximate analysis of strain concentration by notches and cracks, J. Appl. Mech., 35(1968), 379--386.
[Ri68-2] J.R. Rice, Mathematical analysis in the mechanics of fracture, Fracture Volume II, Academic Press, 1968, 191--311.
[Pi84] O. Pironneau, Optimal shape design for elliptic systems, Springer-Verlag, 1984.
[Sa99] J.A. Samareh, A survey of shape parameterization techniques, NASA Report CP-1999-209136 (1999), 333--343.
[Sc91] B.-W. Schulze, Pseudo-differential operators on manifolds with singularities, North-Holland, 1991.
[Sok92] J. Sokolowski and J.-P. Zolesio, Introduction to shape optimization, Springer, 1992.
[St14] K. Sturm, On shape optimization with non-linear partial differential equations, Doctoral thesis, Technische Universiltät of Berlin, 2014. https://d-nb.info/106856959X/34
[Sumi] Y. Sumi, Mathematical and computational analyses of cracking formation, Springer, 2014.
[Zei/2B] E. Zeidler. Nonlinear functional analysis and its applications II/B, Springer, 1990.
[Z-S73] O.C. Zienkiewicz and J.S. Campbell, Shape optimization and sequential linear programming, Optimum Structural Design, Wiley, 1973, 109--126.

top