Shape sensitivity of energy
Method of the Lagrange multiplier
Shape optimization in Stokes problem can not be handled in $V^{\varphi _t}(\Omega (t))$, because the mapping technique does not preserve the property $\textrm{div}u=0$ in general. A similar difficulty was also in the fracture problem with the non-penetration condition $$ V(\Omega )=\{v\in H^1(\Omega ;\mathbb{R}^d):\, (v^+-v^-)\cdot \nu \ge 0 \textrm{ on }\Sigma , v=0\textrm{ on }\Gamma _D\}$$ The difficulty is solved by using the method of the Lagrange multiplier [Ko06]. Here we show the method [K-O18] used in [Ko06], which is related to Correa-Seeger theorem [Co85] stated in Remark 2.11 . Let us set $V(\Omega ):=\{v\in H^1(\Omega ;\mathbb{R}^d):\, v=0\textrm{ on }\Gamma _D\}$, \begin{eqnarray} K^{\varphi _t}(\Omega (t))&:=&\{v\circ \varphi _t^{-1}:\, v\in K(\Omega )\} ,\\ K(\Omega )&:=&\{v\in V(\Omega ):\, \textrm{div}v=0\textrm{ in }\Omega \} \notag \\ K_t(\Omega (t))&:=&\{v\in H^1(\Omega (t);\mathbb{R}^d):\, \textrm{div}v=0\textrm{ in }\Omega (t),~v=0\textrm{ on }\Gamma _D(t)\} , \tag{2.38a} \end{eqnarray} We cannot apply Corollary 2.13 to the Stokes problem, because $K_t(\Omega (t))\neq K^{\varphi _t}(\Omega (t))$ in general and $\mathcal{E}(u(t);f,g,(\Omega ))$ is given by \begin{equation} \mathcal{E}(u(t);f,g,\Omega )=\min _{v\in K_t(\Omega (t))}\mathcal{E}(v;f,g,\Omega (t)) \tag{2.39} \end{equation} with $\widehat{W}(\nabla v)=\frac{\nu }{2} \sum _{i=1}^d |\nabla v_i |^2, v=(v_1,…,v_d)$ where the constant $\nu $ is the flow viscosity. The solution $u(t)$ is obtained as the saddle point $(u(t),p(t))$ of Lagrangian function defined on $V^{\varphi _t}(\Omega (t))\times L^2(\Omega (t);\mathbb{R}^d)$ \begin{eqnarray} \mathcal{L}(u(t),p(t);\Omega (t))&=&\min _{w\in V_t(\Omega (t))}\max _{\lambda \in K_t^*(\Omega (t))}\mathcal{L}(w,\lambda ;\Omega (t))\\ \mathcal{L}(w,\lambda ;\Omega (t))&:=& \mathcal{E}(w;f,g,\Omega (t))-(\lambda ,\textrm{div}w)_{\Omega (t)} \notag \tag{2.40} \end{eqnarray} where $K_t^*(\Omega (t))=\{\lambda \in L^2(\Omega ):\, (\lambda ,\textrm{div}v)_{\Omega (t)}=0 ∀v\in K_t(\Omega (t))\}$. Now we have the following by setting $(u,p)=(u(0),p(0))$. [Coro.2.2, K-O18]
In case of $\Gamma _D=\partial \Omega $, that is, $V_t(\Omega (t))=H^1_0(\Omega (t);\mathbb{R}^d)$, $$ K_t^*(\Omega (t))=\{q\in L^2(\Omega (t)):\, (q,1)_{\Omega (t)}=0\}$$ $[\lambda \mapsto \lambda \circ \varphi _t]$ is not bijective. However, if the surface measure $|\Gamma _N |$ of $\Gamma _N$ is positive, then $K_0^*(\Omega )=L^2(\Omega )$. So we can apply Corollary 2.15
if $|\Gamma _N | \gt 0$. GJ-integral $J^S_{\omega }((u,p),\mu )$ of the Stokes problem is the sum of the surface integral and the volume integral
\begin{eqnarray} &&P^S_{\omega }((u,p),\mu )= \int _{\partial (\omega \cap \Omega )}\left \{\widehat{W}(u)(\mu \cdot n)- (\nu \frac{\partial u}{\partial n}-pn)\cdot (\nabla u\cdot \mu )\right \} ds \tag{2.42a}
\end{eqnarray}
\begin{eqnarray} &&R^S_{\omega }((u,p),\mu )=-\int _{\omega \cap \Omega }\lbrace f\cdot (\nabla u\cdot \mu ) +p{\rm tr}(\nabla \mu \nabla u)\} dx\tag{2.42b}\\ && -\int _{\omega \cap \Omega }\{\widehat{W}(u){\rm div}\mu -[\nu \nabla u\nabla \mu ]:\nabla u\} dx\notag
\end{eqnarray} $R_{\omega }^S((u,p),\mu )$ is finite for all weak solutions $u$. As shown in Theorem 2.2
, if $(u,p)$ is regular, then $J_{\omega }^S((u,p),\mu )=0$ for all $\mu \in W^{1,\infty }(\Omega ;\mathbb{R}^d)$. Theorem 2.15
is rewriten as follows.
Theorem 2.15
If $[\lambda \mapsto \lambda \circ \varphi _t]$ is bijective from $K_t^*(\Omega (t))$ onto $K^*(\Omega )$, then by putting $Bv=\textrm{div}v$
\begin{eqnarray} \frac{d}{dt}\mathcal{E}(u(t);f,g,\Omega (t))|_{t=0} =-R_{\Omega }(u,\mu _{\varphi })-(p,B^1u)_{\Omega } \tag{2.41}
\end{eqnarray} where $(\lambda ,Bw)_{\Omega (t)}=(\lambda \circ \varphi _t,[B+tB^1+B_t^2](v\circ \varphi _t))_{\Omega }$ with linear bounded operators $B^1, B^2_t$ from $V(\Omega )$ to $L^2(\Omega ;\mathbb{R}^d)$, and the residual $B_t^2$ satisfies $$ \|B_t^2 v\|_{0,\Omega }\le c_{RB}\| v\|_{1,\Omega },~0\le c_{RB}(t)=o(t)$$ Corollary 2.16
Let $(u,p)$ be the saddle point of (2.40)
when $|\Gamma _N | \gt 0$. If $\varphi _t(\textrm{supp}_{\Gamma _N}g)=\textrm{supp}_{\Gamma _N}g$ for all $t$, then
\begin{eqnarray} {\textstyle \frac{d}{dt}}\mathcal{E}(u(t);f,g,\Omega (t))|_{t=0}&=& -R_{\Omega }^S((u,p),\mu _{\varphi })\notag \\ &&-\int _{\partial \Omega }fu(\mu _{\varphi }\cdot n)ds \tag{2.43}
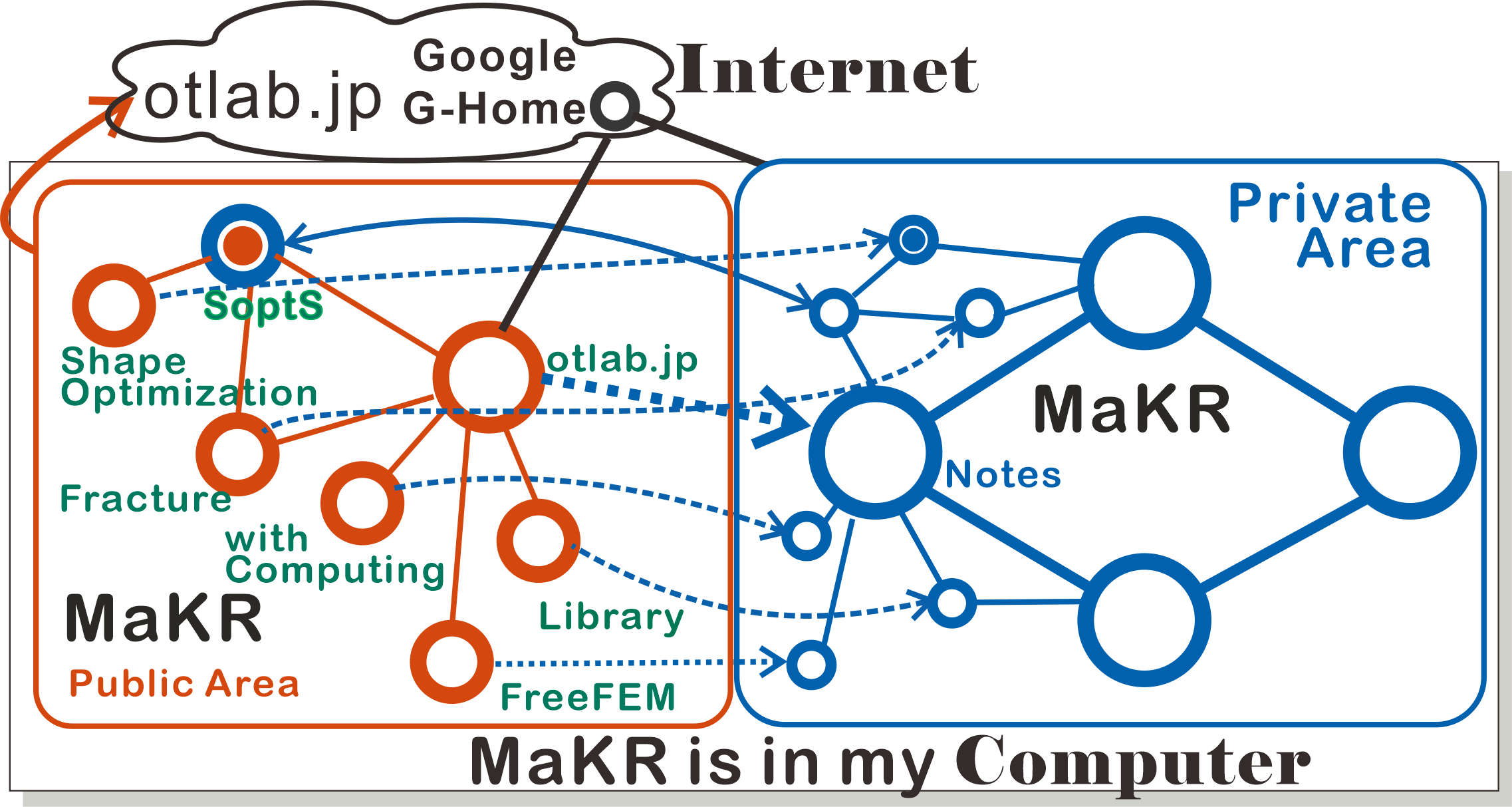
\end{eqnarray} Information about the page: The current position is painted circle in the diagram below. Blue is the main MaKR and orange is a duplicate for MaKR's public use, where dashed line means the connection to the private area The dashed lines are only connections to main MaKR.