Shape sensitivity of energy
GJ-integral
Let $\omega \subset \mathbb{R}^d$ be a domain with Lipschitz property and consider the vector $\mu \in W^{1,\infty }(\mathbb{R}^d;\mathbb{R}^d)$. For the solution $u$ in (2.1) , the GJ-integral $J_{\omega }(u,\mu )$ is defined by \begin{eqnarray} J_{\omega }(u,\mu )&:=&P_{\omega }(u,\mu )+R_{\omega }(u,\mu ), \tag{2.5a} \end{eqnarray} \begin{eqnarray} P_{\omega }(u,\mu )& :=&\int _{\partial (\omega \cap \Omega )}\left \lbrace \widehat{W}(u)(\mu \cdot n)-\widehat{T}(u)(\nabla u\cdot \mu )\right \} \,ds, \tag{2.5b} \end{eqnarray} \begin{eqnarray} R_{\omega }(u,\mu )& :=&-\int _{\omega \cap \Omega }\left \lbrace \nabla _{\xi }\widehat{W}(u)\cdot \mu +f(\nabla u\cdot \mu )\right \} dx\notag \\ && +\int _{\omega \cap \Omega }\left \{ \nabla _{\zeta }\widehat{W}(u):[\nabla u\nabla \mu ]-\widehat{W}(u)\,\textrm{div}\mu \right \} \,dx, \notag \tag{2.5c} \end{eqnarray} \begin{eqnarray} \widehat{T}(u)&:=&(\widehat{T}_{i}(u))_{i=1,…, m}, \widehat{T}_i(u)=\sum _{j=1}^d [\partial \widehat{W}(u)/\partial \zeta _{ij}]n_j, \notag \tag{2.5d} \end{eqnarray} where $n=(n_1,…,n_d)$ is the ourward unit normal vector to $\partial (\omega \cap \Omega )$. For a set $B$ we also use the notation \begin{eqnarray} P_{\omega }(u,\mu |B)& :=&\int _{\partial (\omega \cap \Omega )\cap B}\left \lbrace \widehat{W}(u)(\mu \cdot n)-\widehat{T}(u)(\nabla u\cdot \mu )\right \} \,ds \tag{2.6} \end{eqnarray} and $J_{\omega }(u,\mu |B):=P_{\omega }(u,\mu |B)+R_{\omega }(u,\mu )$. Sometimes we use $P_{\omega }(u,\mu |\partial \omega )$ whose integration region do not contain $\omega \cap \partial \Omega $, because $\omega \cap \partial \Omega \subset \partial (\omega \cap \Omega )\setminus (\partial \omega \cap \Omega )$.Poisson equation
The GJ-integral of the Poisson equation $-\Delta u=f$ is
\begin{eqnarray} P_{\omega }(u,\mu )&=& \int _{\partial (\omega \cap \Omega )}\left \{\frac{1}{2}|\nabla u |^2(\mu \cdot n)-\frac{\partial u}{\partial n}(\nabla u\cdot \mu )\right \} ds\notag \\ R_{\omega }(u,\mu )&=&- \int _{\omega \cap \Omega }\left \lbrace f(\nabla u\cdot \mu )-(\nabla u\cdot \nabla \mu _k)\partial _k u+\frac{1}{2}|\nabla u |^2\textrm{div }\mu \right \} dx \tag{2.7}
\end{eqnarray}
Linear elasticity
The GJ-integral of linear elasticity is
\begin{eqnarray*} P_{\omega }(u,\mu ) &=&\int _{\partial (\omega \cap \Omega )}\left \{ \frac{1}{ 2}\sigma _{ij}(u)e_{ij}(u)(\mu \cdot n)-\sigma _{ij}n_{j}(\nabla u_{i}\cdot \mu )\right \} ds \\ R_{\omega }(u,\mu ) &=&-\int _{\omega \cap \Omega }\left \{ \frac{1}{2}(\mu \cdot \nabla C_{ijkl})e_{kl}(u)e_{ij}(u)+f_{i}(\nabla u_{i}\cdot \mu )\right . \\ &&-\left . \sigma _{ij}(u)\partial _{j}\mu _{k}\partial _{k}u_{i}+ \frac{1}{2}\sigma _{ij}(u)e_{ij}(u)\textrm{div}\mu \right \} dx
\end{eqnarray*} $R_{\omega }(u,\mu )$ is finite for all weak solutions $u$, but $P_{\omega }(u,\mu )$ need regurality of $u$ to be finite. We now prove (GJ-2), and (GJ-1) can be seen from the proof.
GJ=0 if u is regular
Theorem 2.2
If the weak solution $u$ is regular inside $\omega $ and $\omega \cap \Omega $ is the domain with the Lipschitz property, then
\begin{equation} J_\omega (u,\mu )=0~~\textrm{for all } \mu \in W^{1,\infty }(\mathbb{R}^d;\mathbb{R}^d) \tag{2.9}
\end{equation} Proof Since $u |_{\omega \cap \Omega }\in H^2(\omega \cap \Omega ;\mathbb{R}^d)$, $\nabla _x\widehat{W}(x,u(x),\nabla u(x))\cdot \mu (x)$ is written by the chain rule as follows
\begin{eqnarray} && \nabla _{\xi }\widehat{W}(u)\cdot \mu + \widehat{W}_z(u)(\nabla u\cdot \mu )+\nabla _{\zeta }\widehat{W}(u):[\nabla (\nabla u)\cdot \mu ]\notag \\ && =\nabla _{\xi }\widehat{W}(u)\cdot \mu +\widehat{W}_{z}(u)(\nabla u\cdot \mu )\notag \\ && + \nabla _{\zeta }\widehat{W}(u):[\nabla (\nabla u\cdot \mu )] -\nabla _{\zeta }\widehat{W}(u):[\nabla u\nabla \mu ]\notag \tag{2.10}
\end{eqnarray} Using divergence theorem, we have
\begin{eqnarray} \int _{\omega \cap \Omega }\nabla _x\widehat{W}(u)\cdot \mu \, dx &=&\int _{\partial (\omega \cap \Omega )}\widehat{W}(u)(\mu \cdot n)\,ds\notag \\ &&-\int _{\omega \cap \Omega }\widehat{W}(u)\textrm{div}\mu \, dx \tag{2.11}
\end{eqnarray} Since $u$ is regular inside $\omega $, we have by Green's formula
\begin{eqnarray} &&\int _{\omega \cap \Omega }\left \{\widehat{W}_z(u)(\nabla u\cdot \mu )+ \nabla _{\zeta }\widehat{W}(u):[\nabla (\nabla u\cdot \mu )]\right \} dx\notag \\ && =\int _{\partial (\omega \cap \Omega )}\widehat{T}(x,u)(\nabla u\cdot \mu )ds +\int _{\omega \cap \Omega }\left [ -\textrm{div}\nabla _{\zeta }\widehat{W}(u)+\widehat{W}_z(u)\right ](\nabla u\cdot \mu )dx\notag \\ && = \int _{\partial (\omega \cap \Omega )}\widehat{T}(u)(\nabla u\cdot \mu )ds+\int _{\omega \cap \Omega }f(\nabla u\cdot \mu )dx\notag \tag{2.12}
\end{eqnarray} Here we used (2.4)
. Combining (2.10)
,(2.11)
and (2.12)
, we arrive at (2.9)
. ∎
Domain independence
Corollary 2.3
Let $\omega _1,\omega _2$ be two domains such that $\overline{\omega _1}\subset \omega _2$. If $u$ is regular inside $(\omega _2\setminus \overline{\omega _1})\cap \Omega $, and $(\omega _2\setminus \overline{\omega _1})\cap \Omega $ has the Lipschitz property, then $J_{\omega _1}(u,\mu )=J_{\omega _2}(u,\mu )$. 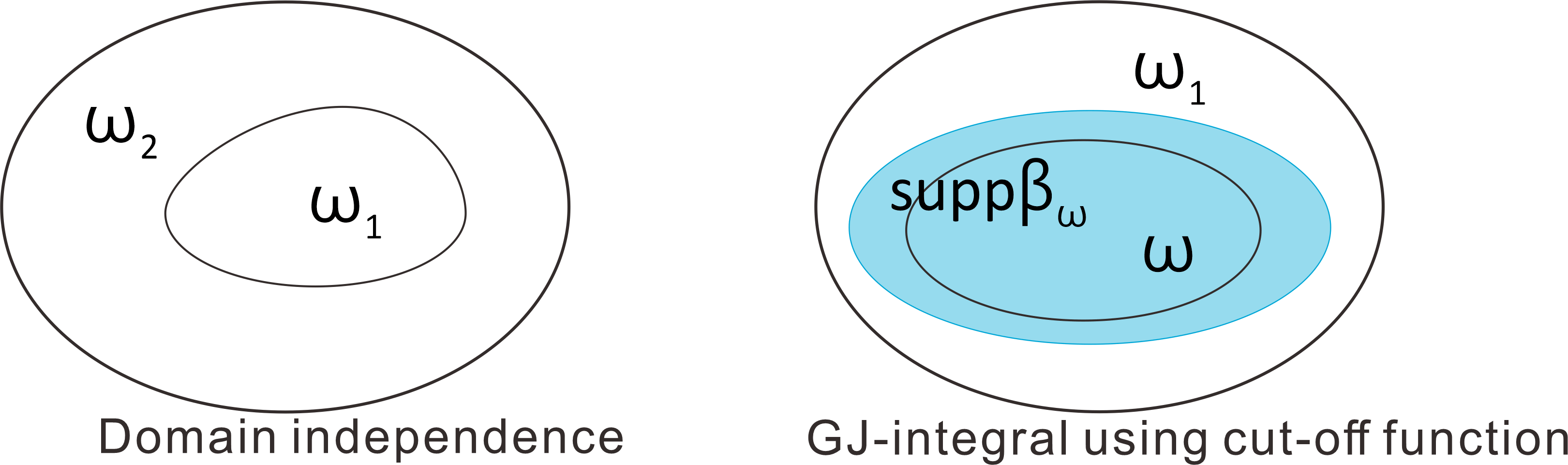
GJ-integral using cut-off
Corollary 2.4
Let $\omega $ be an open set such that $\omega \cap \Omega $ has the Lipschitz property and $\beta _{\omega }\in C^\infty _0(\mathbb{R}^d)$ the cut-off function that is $\beta _{\omega }(x)=1$ for all $x\in \omega ; \beta _{\omega }\ge 0$ and $\beta _{\omega }(x)=0$ for all $x\in \mathbb{R}^d\setminus \overline{\omega _1}$ with an open set $\omega _1, \overline{\omega }\subset \omega _1$. If $u$ is regular inside $\omega _1\setminus \overline{\omega }$, then
\begin{equation} J_{\omega }(u;\mu )=R_{\omega _1}(u;\beta _{\omega }\mu )~~ \textrm{for all }\mu \in W^{1,\infty }(\mathbb{R}^d;\mathbb{R}^d) \tag{2.13}
\end{equation} The weak solution $u$ has `interior regularity' if $u |_{\omega }$ is in $H^2(\omega ;\mathbb{R}^m)$ and satisfy (2.4)
for an arbitrary $\omega $ such that $\overline{\omega }\subset \Omega $.
Limit when GJ = 0
In crack problems, there is a solution $u\in H^{3/2-\epsilon }(\Omega ;\mathbb{R}^2), \epsilon \gt 0$ such that $J_{\omega }(u,e_1)\neq 0$ in (2.20)
, but if the solution $u$ of (2.1)
has more smoothness, we can show the following using the Trace theorem [2.4, Nec67].
Theorem 2.6
If the weak solution $u$ has interior regularity, and $\omega \cap \Omega $ is the domain with the Lipschitz property and $u_{\omega \cap \Omega }\in H^{\alpha }(\omega \cap \Omega ;\mathbb{R}^m)$ for any $\alpha \gt 3/2$, then
\begin{equation} J_\omega (u,\mu )=0~~\textrm{for all } \mu \in W^{1,\infty }(\mathbb{R}^d;\mathbb{R}^d) \tag{2.14}
\end{equation} 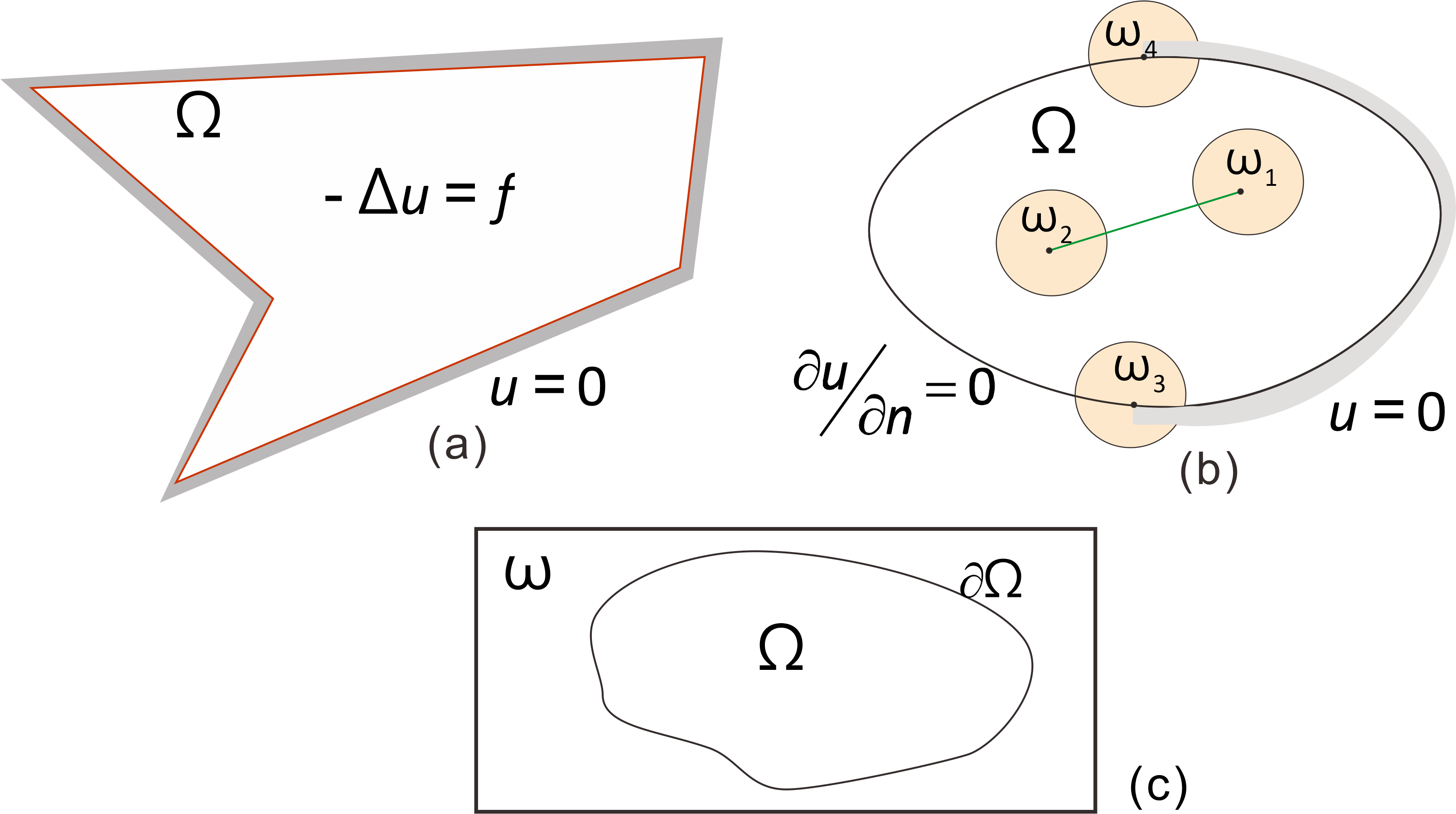
- (a)
- The solution $u$ of the Poisson equation with Dirichlet boundary condiotion in the polygonal domain is $u\in H^{\alpha }(\Omega ), \alpha \gt 3/2$, so $J_{\Omega }(u.\mu )=0$ [Gr92].
- (b)
- There is a solution $u$ of the Poisson equation with Mixed boundary condiotion and the crack such that $J_{\omega _i}(u,(-1)^{i-1}e_1)\neq 0, i=1,2$ and $J_{\omega _i}(u,\mu )\neq 0$, $e_1(1,0)$.
- (c)
- If $\overline{\Omega }\subset \omega $, then $J_{\omega }(u,\mu ):=R_{\Omega }(u,\mu )$.
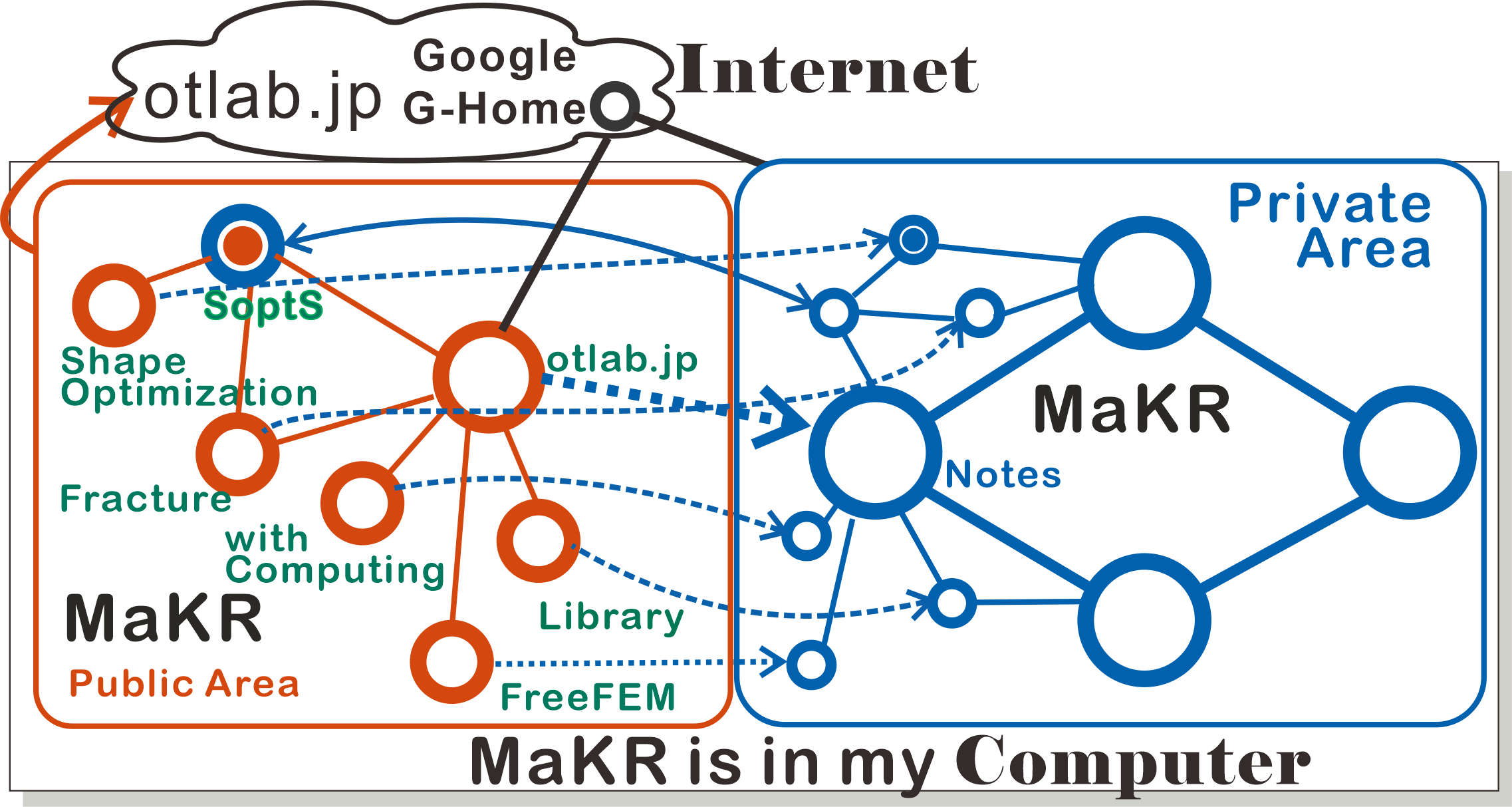
Information about the page: The current position is painted circle in the diagram below. Blue is the main MaKR and orange is a duplicate for MaKR's public use, where dashed line means the connection to the private area The dashed lines are only connections to main MaKR.