Shape sensitivity of energy
We describe the definition of the GJ-integral and the relation with fracture mechanics in Section 2.2 , and prove properties (GJ-1) and (GJ-2) in Theorem 2.2 and (GJ-3) is given in Theorem 2.8 in linear case using the first method and is given in Corollary 2.13 after showing the differentiability of functional (Theorem 2.10 ) with respect to a parameter in an abstract framework. Let $\widehat{W}(\xi ,z,\zeta )$ be a function defined for almost all $\xi \in \mathbb{R}^d$ and for all $z\in \mathbb{R}^m (m\ge 1), \zeta \in \mathbb{R}^{m\times d}$. For a measurable functions $v_i=v_i(x) (x\in \Omega , i=1,…m)$, the operator $[v\mapsto \widehat{W}(x,v(x),\nabla v(x))]$ is defined by the formula $$ \widehat{W}(x,v(x),\nabla v(x))=\widehat{W}(\xi ,z,\zeta ), \xi =x, z=v(x), \zeta =\nabla v(x) \textrm{for }x\in \Omega $$ In the followsing we shall use $\widehat{W}(v)$ for $\widehat{W}(x,v,\nabla v)$ when there is no ambiguity. For a given functions $f\in L^2(\Omega ;\mathbb{R}^m), g\in H^1(\Omega ;\mathbb{R}^m)$, the weak solution $u$ is the minimization of the energy functional \begin{eqnarray} \mathcal{E}(u;f,g,\Omega )&=&\min _{v\in V(\Omega )}\mathcal{E}(v;f,g,\Omega ) \tag{2.1} \end{eqnarray} \begin{eqnarray} \mathcal{E}(v;f,g,\Omega )&:=&\int _{\Omega }\{\widehat{W}(v)-fv\} dx- \int _{\Gamma _N}gv\, ds \tag{2.2} \end{eqnarray} over a subset $V(\Omega )$ of $H^1(\Omega ;\mathbb{R}^m)$ where $\Gamma _N$ is the part of $\partial \Omega $, which leads $\mathcal{L}(u)=f$ given in ((2.4) ). For simplicity, we used $L^2(\Omega ;\mathbb{R}^m), H^1(\Omega ;\mathbb{R}^m)$, but we can formulate them for nonlinear equations by using $L^p(\Omega ;\mathbb{R}^m), W^{1,p}(\Omega ;\mathbb{R}^m)$ with $p\ge 1$. The following are examples of $\mathcal{L}, \widehat{W}$. Partial differential equations $(m=1)$:Partial differential equations
Poisson's equation:
$-\Delta u=f,\mathcal{L}(u)=-\Delta u$;$\widehat{W}(\xi ,z,\zeta )=|\zeta |^2/2$, $\widehat{W}(v)=\frac{1}{2}|\nabla v |^2$.If $V(\Omega )=H_0^1(\Omega ):=\{v\in H^1(\Omega ):v=0\textrm{ on }\partial \Omega \}$ then $$ -\Delta u(x) = f(x)~~x\in \Omega ;~~u(x)=0~~x\in \partial \Omega $$
Linear elliptic equation:
$\mathcal{L}(u)=-\partial _i (a_{ij}(x)\partial _j u)+q(x)u, a_{ij}=a_{ji}$; $\widehat{W}(\xi ,z,\zeta )=(a_{ij}(\xi )\zeta _i\zeta _j+q(\xi )z^2)/2$, $\widehat{W}(v)=\frac{1}{2}(a_{ij}(x)\partial _iv\partial _jv+q(x)v^2)$ with ellipticity $a_{ij}\zeta _i\zeta _j \gt 0 ∀\zeta \in \mathbb{R}^d\setminus \{0\}$. If $V(\Omega )=H_0^1(\Omega ,\Gamma _D):=\{v\in H^1(\Omega ):~u=0~\textrm{on }\Gamma _D\}$ then $$ -\sum _{i,j=1}^d \partial _i a_{ij}\partial _j u + q(x)u(x)= f~~\textrm{in }\Omega ;~~u=0~~\textrm{on }\Gamma _D;~$$
Partial differential system $(m \gt 1)$
Vector Poisson:
$-\Delta u_i=f_i$ with $u=(u_1,…,u_m), \mathcal{L}=(\mathcal{L}_1,…,\mathcal{L}_m), m \gt 1$; $\mathcal{L}_i(u)= -\Delta u_i, \widehat{W}(\xi ,z,\zeta )=\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^d\zeta _{ij}^2$.
Linear elasticity:
$\mathcal{L}=(\mathcal{L}_1,…,\mathcal{L}_d)$, $\mathcal{L}_i(u)=-\partial _j \sigma _{ij}(x,u), \sigma _{ij}(x,u)=C_{ijkl}e_{kl}(u)$; $\widehat{W}(\xi ,z,\zeta )=\frac{1}{2}C_{ijkl}(\xi )e_{kl}(\zeta )e_{ij}(\zeta )$, $e_{ij}(\zeta )=\frac{1}{2}(\zeta _{i,j}+\zeta _{j,i})$ with Hooke's tensor $C_{ijkl}(\xi )$ having symmetry $C_{ijkl}=C_{jilk}=C_{klij}$ satisfying ellipticity $C_{ijkl}e_{kl}e_{ij} \gt \alpha e_{ij}e_{ij}$ with a number $\alpha \gt 0$ for all non zero $(e_{ij})$. The material is called homogeneous, if Hooke's tensor $C_{ijkl}$ are constant, that is, $\widehat{W}(\xi ,z,\zeta )$ is indenpendent of $\xi $. When the material is isotropic, $C_{ijkl}=\lambda \delta _{ij}\delta _{kl}+ G(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})$ with Kronecker delta $\delta _{ij}$ and Lame's constants $\lambda ,G$ and $\widehat{W}(v)=\frac{1}{2}\lambda ({\rm div}v)^2+G e_{ij}e_{ij}$. The ellipticity hold if $G \gt 0, 3\lambda +2G \gt 0$.
Hyperelasticity:
$-\partial _j\sigma _{ij}(x,u)=f_i, \sigma _{ij}(x,u)=\partial \widehat{W}(u)/\partial e_{ij}$. Hyperelastic material contains nonlinearities (e.g. [Cir88]).
In the above examples, we assumed that $[(\xi ,z,\zeta )\mapsto \widehat{W}(\xi ,z,\zeta )]\in C^1(\mathbb{R}^d\times \mathbb{R}^m\times \mathbb{R}^{m\times d})$. Let us denote with $v\in V(\Omega )$
\begin{equation*} \delta \widehat{W}(u)[v]:=\lim _{\epsilon →0}\epsilon ^{-1} \left [\widehat{W}(u+\epsilon v)-\widehat{W}(u)\right ]
\end{equation*} when $u+\epsilon v\in V(\Omega )$ for small $\epsilon $. Then we have
\begin{equation} \lim _{\epsilon →0}\epsilon ^{-1}\left [\mathcal{E}(u+\epsilon v;f,g,\Omega )- \mathcal{E}(u;f,g,\Omega )\right ] =\int _{\Omega }\{\delta \widehat{W}(u)[v]-fv\} dx-\int _{\Gamma _N}gv\, ds \tag{2.3}
\end{equation} The problem (2.1)
is called linear if $V(\Omega )$ is the closed subspace of $H^1(\Omega ;\mathbb{R}^m)$ and $a(w,v)=\int _{\Omega }\delta \widehat{W}(w)[v]dx$ is bilinear form on $V(\Omega )\times V(\Omega )$. For a given open set $\omega \subset \mathbb{R}^d$, if $u |_{\omega \cap \Omega }\in H^2(\omega \cap \Omega ;\mathbb{R}^m), u±\epsilon v\in V(\Omega ) ∀v\in C_0^\infty (\omega \cap \Omega ;\mathbb{R}^m)$ with $|\epsilon |\le \epsilon _0, \textrm{small }\epsilon _0 \gt 0$, then we obtain the partial differential equation/system $\mathcal{L}(u)=f$
\begin{equation} -\textrm{div}\left [\nabla _\zeta \widehat{W}(u)\right ] +\widehat{W}_z(u)=f \textrm{in }L^2(\omega \cap \Omega ;\mathbb{R}^m) \tag{2.4}
\end{equation} where
\begin{eqnarray*} \nabla _{\zeta }\widehat{W}(x,z,\zeta )&:=&\left (\array{\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{1,1}&…&\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{1,d}\\ \vdots &\ddots &\vdots \\ \partial \widehat{W}(x,z,\zeta )/\partial \zeta _{m,1}&…&\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{m,d} }\right )\\ \textrm{div}\left [\nabla _\zeta \widehat{W}(u)\right ]&=&\left (\array{\partial _1[\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{1,1}]+&…&+\partial _d [\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{1,d}]\\ &\vdots &\\ \partial _1[\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{m,1}]+&…&+\partial _d [\partial \widehat{W}(x,z,\zeta )/\partial \zeta _{m,d}] }\right )\\ \widehat{W}_z(x,z,\zeta )&:=&\partial \widehat{W}/\partial z \textrm{if }m=1; :=(\partial \widehat{W}/\partial z_1,…,\partial \widehat{W}/\partial z_m)^T \textrm{if }m \gt 1
\end{eqnarray*}
The solution $u$ obtained by (2.1)
is called `regular inside $\omega $' if $u |_{\omega \cap \Omega }$ is in $H^2(\omega \cap \Omega ;\mathbb{R}^m)$ and satisfy (2.4)
.
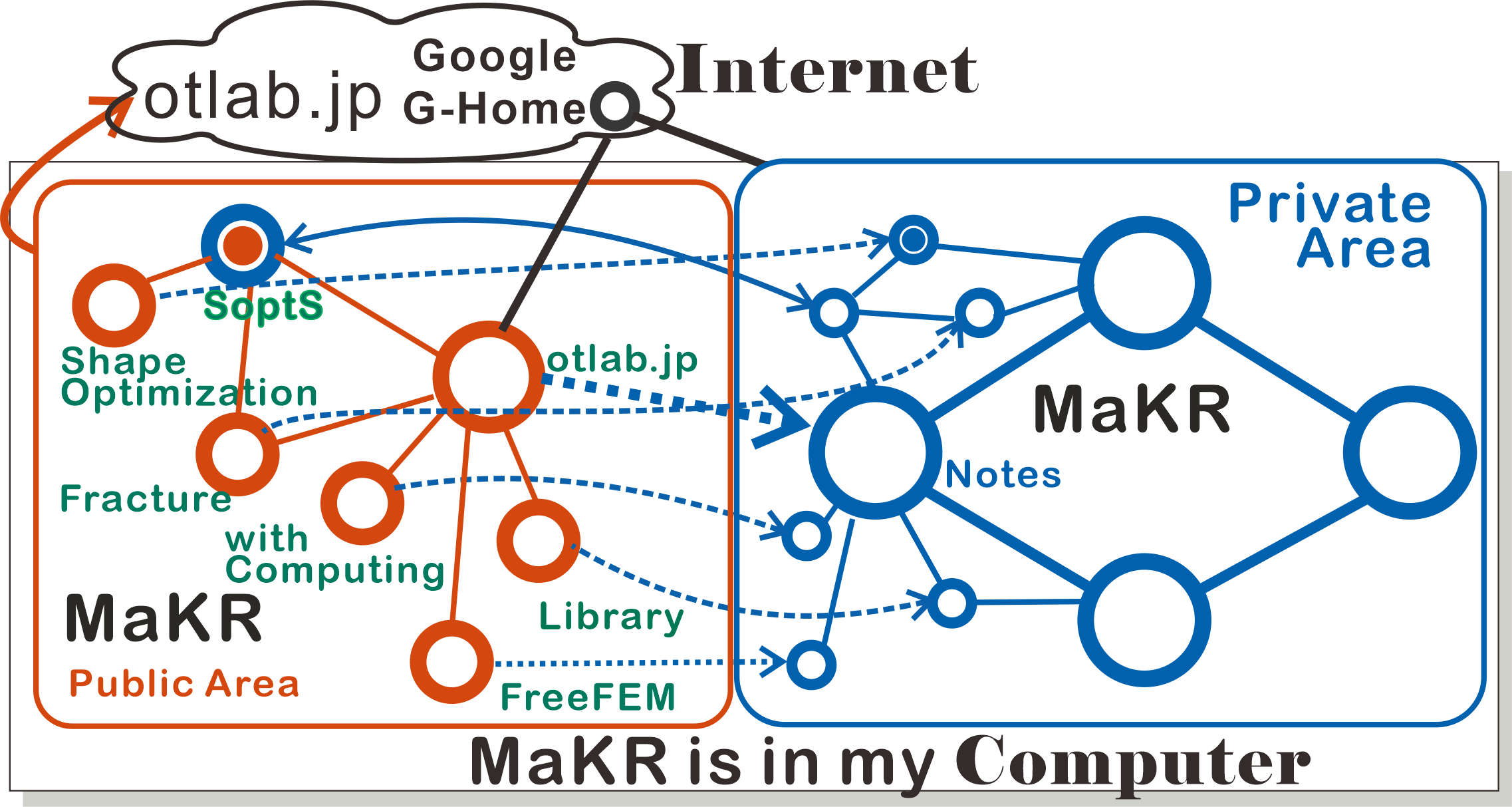
Information about the page: The current position is painted circle in the diagram below. Blue is the main MaKR and orange is a duplicate for MaKR's public use, where dashed line means the connection to the private area The dashed lines are only connections to main MaKR.